Fuso Esférico
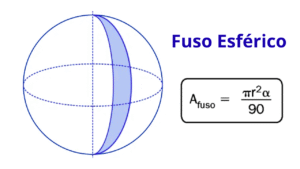
Na geometria espacial, o fuso esférico é uma região da superfície da esfera delimitada por dois semicírculos que têm o mesmo diâmetro. É como uma “fatia” da esfera, semelhante aos fusos horários do globo terrestre.
1) Definição
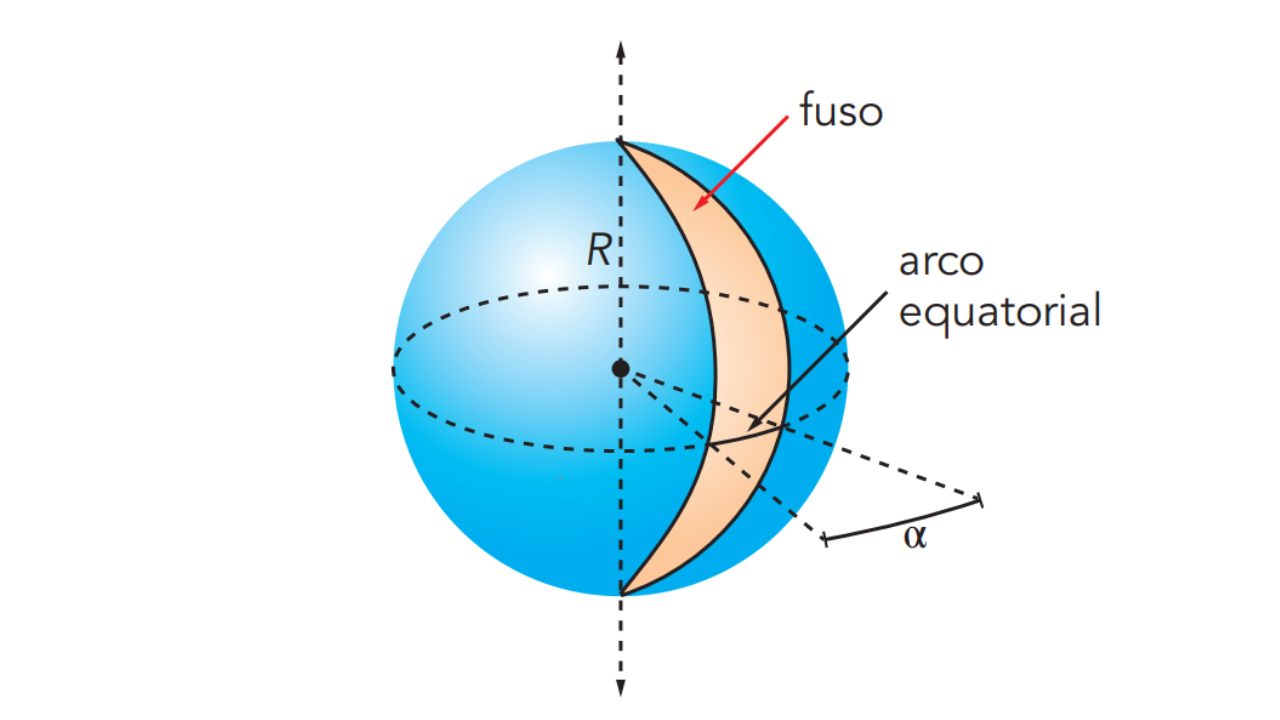
Considere uma esfera de raio \(R\). Se tomarmos dois planos que passam pelo eixo da esfera, o espaço compreendido entre esses planos, limitado pela superfície esférica, forma um fuso esférico.
- Ângulo central (\(\alpha\)): ângulo formado pelos dois planos no centro da esfera.
- Arco equatorial: arco da circunferência máxima (equador) compreendido entre os planos.
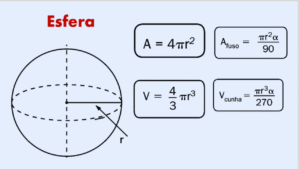
2) Área do fuso esférico
A área do fuso é proporcional ao ângulo central \(\alpha\), em relação à área total da esfera:
Se o ângulo estiver em radianos:
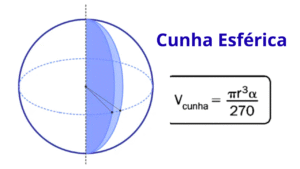
3) Volume da cunha esférica (ou setor esférico)
O setor esférico é o sólido gerado ao girar o fuso esférico em torno do eixo da esfera. Seu volume também é proporcional ao ângulo \(\alpha\):
Em radianos:
4) Exemplos resolvidos
Exemplo 1: Determine a área de um fuso esférico de ângulo central \(\alpha=90^\circ\) em uma esfera de raio \(R=6\) cm.
Mostrar solução
\(A=\frac{90}{360}\cdot4\pi R^2=\frac{1}{4}\cdot4\pi\cdot36=36\pi\;\text{cm}^2\).
Exemplo 2: Calcule o volume do setor esférico correspondente a um fuso de \(\alpha=\pi/3\) rad em uma esfera de raio \(R=3\) cm.
Mostrar solução
\(V=\frac{2}{3}\alpha R^3=\frac{2}{3}\cdot\frac{\pi}{3}\cdot27=6\pi\;\text{cm}^3\).
5) Aplicações do fuso esférico
- Geografia: fusos horários são representados por fusos esféricos na superfície terrestre.
- Astronomia: delimitação de áreas no globo celeste.
- Engenharia: cálculos em estruturas esféricas, como cúpulas e reservatórios.
6) Exercícios propostos
1. Calcule a área de um fuso esférico de raio \(R=10\) cm e ângulo central \(\alpha=120^\circ\).
2. Em uma esfera de raio \(R=8\) cm, determine o volume do setor esférico correspondente a \(\alpha=\pi/2\).
7) Links relacionados
Lembre-se: o fuso esférico é para a superfície, e o setor esférico é para o volume.