Geometria Espacial — Poliedros, Corpos Redondos e a Relação de Euler
Neste guia prático de Geometria Espacial você vai identificar rapidamente as famílias de sólidos (poliedros e corpos redondos), entender a Relação de Euler \(V+F=A+2\) e resolver exercícios com passos linha a linha — perfeitos para leitura no celular.
1) O que é Geometria Espacial?
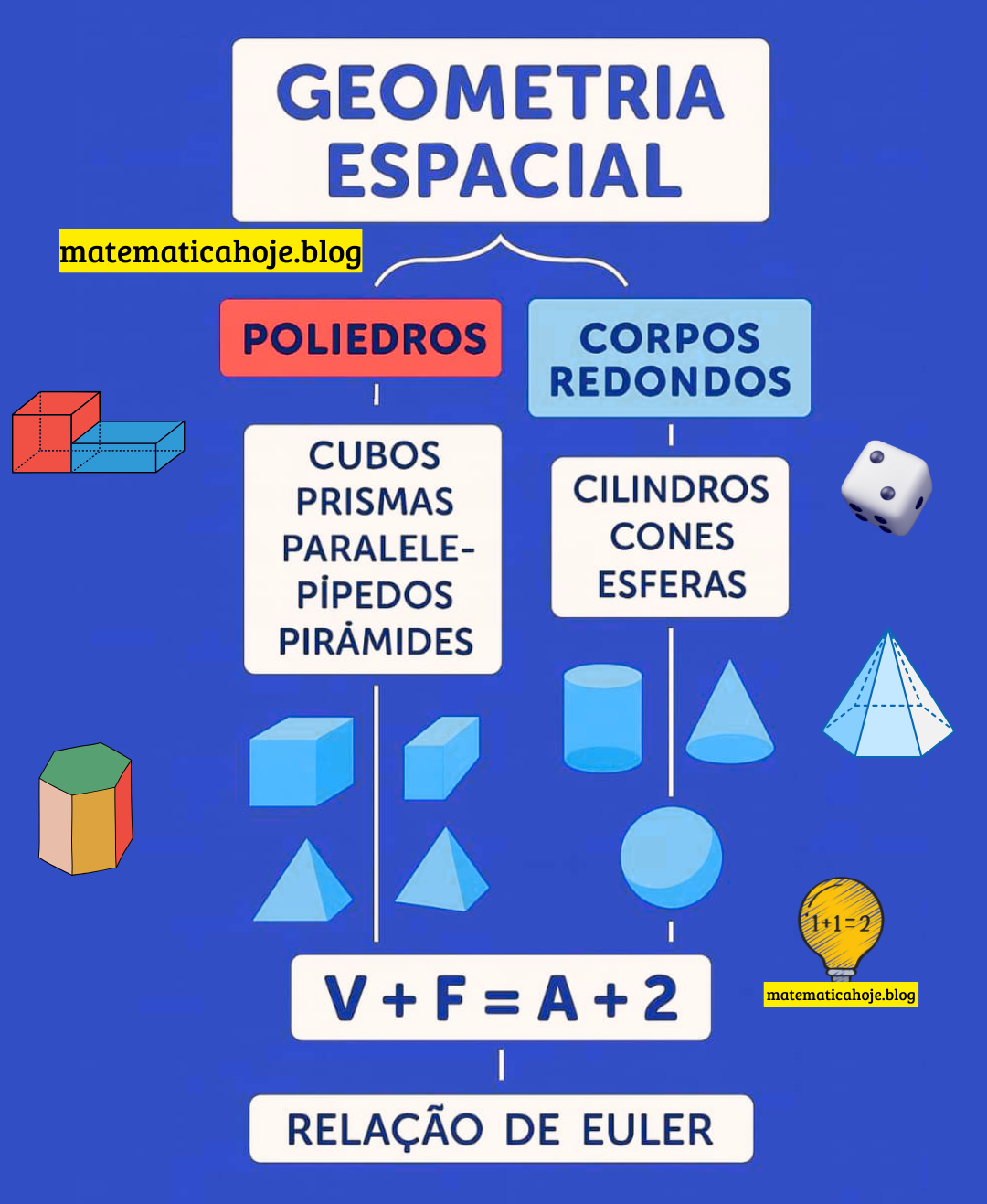
É o ramo da Matemática que estuda as figuras tridimensionais (sólidos) — objetos com largura, altura e profundidade: cubos, prismas, pirâmides, cilindros, cones, esferas, entre outros. Classificamos os sólidos em dois grandes grupos:
Poliedros
Possuem faces planas (polígonos), arestas (encontros das faces) e vértices (pontos de encontro das arestas).
- Cubos e paralelepípedos (prismas retangulares)
- Prismas em geral (bases poligonais paralelas)
- Pirâmides (uma base poligonal e faces laterais triangulares)
Corpos Redondos
Apresentam superfícies curvas. Não possuem faces planas por toda a superfície.
- Cilindros (duas bases circulares paralelas)
- Cones (base circular e um vértice)
- Esferas (todos os pontos à mesma distância do centro)
Dica: identifique se as faces são planas ou curvas. Essa é a chave para decidir se o sólido é poliedro ou corpo redondo.
2) Relação de Euler
Para poliedros convexos, vale a famosa relação:
\( \displaystyle V + F = A + 2 \)
Onde \(V\) = número de vértices, \(F\) = número de faces e \(A\) = número de arestas.
Exemplo 1 — Cubo
Dados: \(V=8\), \(F=6\). Determine \(A\).
👀 Solução passo a passo
\(8 + 6 = A + 2\)
\(14 = A + 2\)
\(A = 14 – 2\)
\(A = 12\)
Exemplo 2 — Pirâmide de base quadrada
Dados: \(V=5\) (4 da base + 1 vértice), \(F=5\) (1 base + 4 faces triangulares). Encontre \(A\).
👀 Solução passo a passo
\(5 + 5 = A + 2\)
\(10 = A + 2\)
\(A = 10 – 2\)
\(A = 8\)
Exemplo 3 — Prisma triangular
Dados: um prisma triangular tem \(V=6\), \(F=5\). Determine \(A\).
👀 Solução passo a passo
\(6 + 5 = A + 2\)
\(11 = A + 2\)
\(A = 11 – 2\)
\(A = 9\)
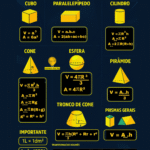
3) Medidas mais usadas em sólidos
Poliedros (idéias-chave)
- Área total = soma das áreas das faces.
- Volume dos prismas: \(V = A_{\text{base}}\cdot h\).
- Volume das pirâmides: \(V = \dfrac{A_{\text{base}}\cdot h}{3}\).
Corpos redondos (idéias-chave)
- Cilindro: \(V=\pi r^2 h\), \(A_T=2\pi r(h+r)\).
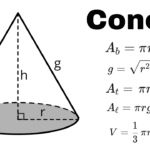
- Cone: \(V=\dfrac{\pi r^2 h}{3}\), \(A_T=\pi r(r+g)\).
- Esfera: \(V=\dfrac{4}{3}\pi r^3\), \(A_T=4\pi r^2\).
Exemplo 4 — Volume do cilindro
Um cilindro tem raio \(r=3\,\text{cm}\) e altura \(h=5\,\text{cm}\). Calcule o volume.
👀 Solução passo a passo
\(V = \pi \cdot 3^2 \cdot 5\)
\(V = \pi \cdot 9 \cdot 5\)
\(V = 45\pi\,\text{cm}^3\)
Exemplo 5 — Pirâmide de base retangular
Base \(6\times4\) e altura \(h=9\). Encontre o volume.
👀 Solução passo a passo
\(A_{\text{base}} = 24\)
\(V = \dfrac{A_{\text{base}}\cdot h}{3}\)
\(V = \dfrac{24\cdot 9}{3}\)
\(V = \dfrac{216}{3}\)
\(V = 72\,\text{u}^3\)
4) Exercícios propostos (com soluções em toggle)
4.1 — Discursivos
Q1. Um prisma hexagonal tem \(V=12\) vértices e \(F=8\) faces. Use a Relação de Euler para determinar o número de arestas \(A\).
👀 Ver solução
\(12 + 8 = A + 2\)
\(20 = A + 2\)
\(A = 20 – 2\)
\(A = 18\)
Q2. Uma pirâmide de base triangular tem aresta da base \(a=4\) e altura \(h=9\). Sabendo que a área da base é \(A_{\text{base}}=\dfrac{\sqrt{3}}{4}a^2\), calcule o volume.
👀 Ver solução
\(A_{\text{base}}=\dfrac{\sqrt{3}}{4}\cdot 16\)
\(A_{\text{base}}=4\sqrt{3}\)
\(V=\dfrac{A_{\text{base}}\cdot h}{3}\)
\(V=\dfrac{4\sqrt{3}\cdot 9}{3}\)
\(V=\dfrac{36\sqrt{3}}{3}\)
\(V=12\sqrt{3}\,\text{u}^3\)
Q3. Um cilindro tem área total \(A_T=2\pi r(h+r)\) igual a \(150\pi\) e raio \(r=5\). Encontre a altura \(h\).
👀 Ver solução
\(150\pi=2\pi\cdot 5(h+5)\)
\(150\pi=10\pi(h+5)\)
\(150=10(h+5)\)
\(15=h+5\)
\(h=10\)
4.2 — Múltipla escolha
Q4. Qual opção não representa um poliedro?
- Cubo
- Prisma
- Pirâmide
- Esfera
👀 Ver gabarito
Q5. Um poliedro convexo possui \(V=10\) e \(A=24\). O número de faces é:
- 10
- 12
- 16
- 18
👀 Ver gabarito
\(10+F=24+2\)
\(10+F=26\)
\(F=16\)
Alternativa C.
Q6. O volume de um cone com \(r=3\) e \(h=12\) é:
- \(12\pi\)
- \(36\pi\)
- \(108\pi\)
- \(144\pi\)
👀 Ver gabarito
\(V=\dfrac{\pi\cdot 3^2\cdot 12}{3}\)
\(V=\dfrac{\pi\cdot 9\cdot 12}{3}\)
\(V=\dfrac{108\pi}{3}\)
\(V=36\pi\)
Alternativa B.
5) Perguntas rápidas (SEO & revisão)
Para quem procura por termos gerais de matemática básica, incluímos frases de busca natural que também aparecem no blog:
- Operações com números inteiros; regras de sinais (adição e subtração de inteiros, multiplicação e divisão com sinais).
- Matemática básica para concursos e ENEM, com jogo de sinais e resolução passo a passo.
Esses temas se conectam à Geometria Espacial quando trabalhamos expressões, unidades e manipulação algébrica nas fórmulas de volume e área.
- ENEM Matemática — revise geometria e medidas que mais caem.
- 10 eBooks de Matemática — teoria + exercícios.
- Banco de Questões — prática com gabarito e comentários.
Conclusão
Você viu como classificar sólidos em poliedros e corpos redondos, aplicou a Relação de Euler e praticou as principais fórmulas de volume e área. O próximo passo é treinar muito com questões.
Baixe agora o eBook gratuito de Fórmulas Matemáticas e acompanhe as novidades no nosso canal do WhatsApp pelo matematicahoje.blog. Bons estudos! ✨