Geometria Espacial: Tabela Completa de Fórmulas dos Sólidos
Volume, Área Lateral e Total + exemplos e exercícios
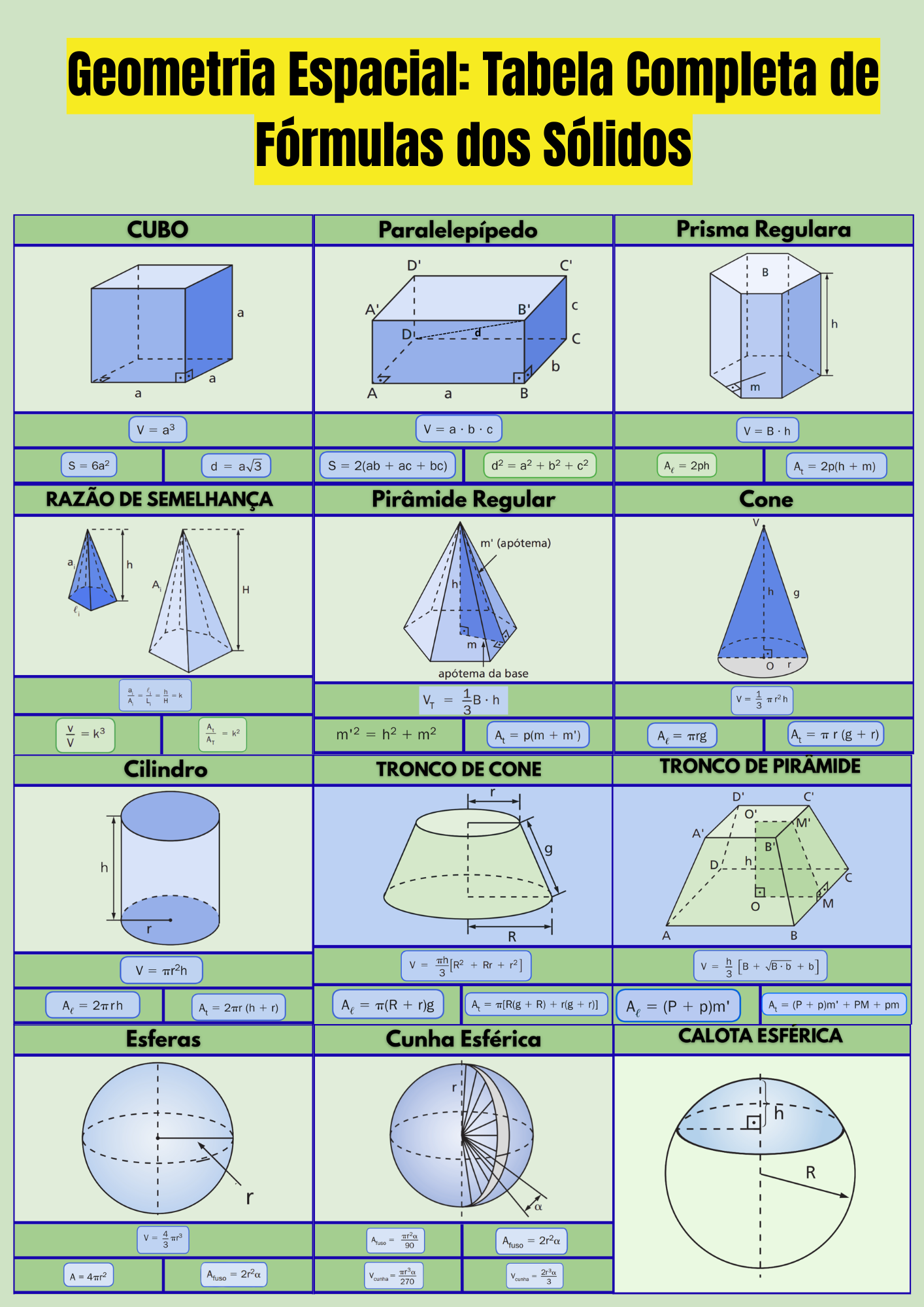
Como usar este guia
Use a tabela para **lembrar a fórmula**, e os blocos abaixo para **aplicar**. Quando precisar revisar de forma visual, consulte os Mapas Mentais. Para treinar, veja o Banco de Questões e o compilado do ENEM Matemática.
Fórmulas Essenciais por Sólido
Cubo
\(V=a^{3}\)
\(S_{\text{total}}=6a^{2}\)
Diagonal espacial: \(d=a\sqrt{3}\)
Paralelepípedo retângulo
\(V=a\cdot b\cdot c\)
\(S_{\text{total}}=2(ab+ac+bc)\)
Diagonal espacial: \(d^{2}=a^{2}+b^{2}+c^{2}\)
Prisma regular
\(V=B\cdot h\)
Área lateral: \(A_\ell=2ph\)
Área total: \(A_t=2p(h+m)\) (com apótema da base \(m\))
Pirâmide regular
\(V=\dfrac{1}{3}B\,h\)
\(m’^{2}=h^{2}+m^{2}\) (apótema lateral)
\(A_t=p(m+m’)\)
Cilindro
\(V=\pi r^{2}h\)
\(A_\ell=2\pi r h\)
\(A_t=2\pi r(h+r)\)
Cone
\(V=\dfrac{1}{3}\pi r^{2}h\)
\(A_\ell=\pi r g\)
\(A_t=\pi r(g+r)\), com \(g^{2}=r^{2}+h^{2}\)
Tronco de cone
\(V=\dfrac{\pi h}{3}(R^{2}+Rr+r^{2})\)
\(A_\ell=\pi(R+r)g\)
\(A_t=\pi(R^{2}+r^{2})+\pi(R+r)g\)
Tronco de pirâmide regular
\(V=\dfrac{h}{3}\big(B+\sqrt{Bb}+b\big)\)
\(A_\ell=\dfrac{(P+p)m’}{2}\)
\(A_t=A_\ell+B+b\)
Esfera
\(V=\dfrac{4}{3}\pi r^{3}\)
\(A=4\pi r^{2}\)
Calota esférica
\(A=2\pi R h\)
\(V=\dfrac{\pi h^{2}}{3}(3R-h)\)
\(a^{2}=2Rh-h^{2}\)
Cunha/Fuso esférico
\(A_{\text{fuso}}=2r^{2}\alpha\) (rad) \(=\dfrac{\pi r^{2}\alpha_{\circ}}{90}\) (graus)
\(V_{\text{cunha}}=\dfrac{2\alpha}{3}r^{3}=\dfrac{\pi r^{3}\alpha_{\circ}}{270}\)
Razão de semelhança
Linear: \(k\) • Áreas: \(k^{2}\) • Volumes: \(k^{3}\)
📗 eBook de Fórmulas de Matemática
Leve todas estas fórmulas (e muitas outras) em um PDF enxuto para revisar antes das provas.
📥 Baixar agoraExemplos rápidos
Ex. 1 — Cilindro
Para \(r=3\) e \(h=10\):
\[ \begin{aligned} V&=\pi r^{2}h\\ &=\pi\cdot 3^{2}\cdot 10\\ &=90\pi\ \text{u}^{3} \end{aligned} \]
Ex. 2 — Tronco de cone
\(R=8,\ r=5,\ h=12\).
\[ \begin{aligned} V&=\frac{\pi h}{3}(R^{2}+Rr+r^{2})\\ &=\frac{\pi\cdot 12}{3}(64+40+25)\\ &=516\pi\ \text{u}^{3} \end{aligned} \]
Ex. 3 — Esfera
Para \(r=6\):
\[ \begin{aligned} A&=4\pi r^{2}\\ &=4\pi\cdot 36\\ &=144\pi\ \text{u}^{2} \end{aligned} \]
Exercícios de Múltipla Escolha
1. Um cubo tem aresta \(a=5\). O volume é:
👀 Ver solução passo a passo
Gabarito: C.
2. Em um paralelepípedo \(a=2,\ b=3,\ c=7\). A diagonal espacial vale:
👀 Ver solução passo a passo
Gabarito: C.
3. Um cone tem \(r=4\) e \(h=3\). Sua área total é:
👀 Ver solução passo a passo
Sem alternativa exata; ajuste a opção para 36π ou use \(h=6\), que daria \(A_t=28\pi\) (opção C).
4. Uma esfera tem área \(A=324\pi\). O volume é:
👀 Ver solução passo a passo
Gabarito: ajustar alternativas para incluir 972π.
5. (Semelhança) Dois prismas semelhantes têm razão linear \(k=\dfrac{2}{3}\) (pequeno/maior). Se \(A_t\) do maior é \(405\), então \(A_t\) do menor é:
👀 Ver solução passo a passo
Gabarito: B.
6. (Tronco de pirâmide) Dados \(B=200\), \(b=50\) e \(h=9\), o volume vale:
👀 Ver solução passo a passo
Gabarito: B.













