1. Introdução
Entre os anos de 2020 e junho de 2025, 13 questões de geometria plana foram aplicadas no vestibular da UNICAMP, representando cerca de 10,81% da prova de matemática. Esse dado evidencia que dominar este tema é essencial para quem deseja uma aprovação na instituição, dado o peso e a frequência contínua de tais questões.
2. Panorama Estatístico
- Total de questões de geometria plana (2020‑2025): 13
- Percentual na prova de matemática: aproximadamente 10,81%
- Média anual: cerca de 2,2 questões por edição
- Implicação: mesmo sendo um tema pontual, tem peso significativo e recorrência constante.
3. Tópicos Frequentes na Geometria Plana da UNICAMP
As questões de geometria plana costumam abordar os seguintes conteúdos:
- Triângulos — semelhança, relações métricas (altura, comparação de lados), cálculo de perímetro e área.
- Quadriláteros e outros polígonos — trapezoides, paralelogramos, retângulos, polígonos regulares.
- Circunferência e círculo — ângulos inscritos, setores, segmentos circulares, cordas, tangentes.
- Compostos e áreas — figuras formadas por sobreposição ou união de formas básicas, cálculo de áreas somadas ou subtraídas.
- Posições relativas e interseções — intersecção de retas, planos, triângulos inscritos em figuras.
Esses temas reaparecem quase todo ano, alternando entre abordagem analítica e geométrica pura.
Geometria Espacial Unicamp Vestibular: O Guia Completo (2020–2025)
4. Metodologias Eficazes para Resolução
Para abordar questões da geometria plana Unicamp vestibular, adote estas estratégias:
- Leitura atenta do desenho: identifique cores, traços auxiliares, medidas indicadas, ângulos e relações de paralelismo ou perpendicularidade.
- Reconheça formas semelhantes: segmente figuras complexas em triângulos ou polígonos menores, aplique semelhança formal (SSS, ÂÂ, SAS).
- Use propriedades métricas: altura em triângulos, razão de áreas, pitagórica, razão entre cordas, triângulo retângulo inscrito.
- Organize a resolução em etapas claras: (a) identificar dado e o que se pede; (b) projetar ou completar construção; (c) aplicar fórmulas ou propriedades geométricas; (d) concluir com razão ou valor numérico.
- Checagem final de consistência: lembre-se de unidades, coerência visual (área não pode ser negativa ou maior que a figura total, por exemplo).
5. Questões Comentadas
A figura a seguir mostra um triângulo \( ABC \) que contém dois quadrados em seu interior. O segmento \( GH \) é lado de um dos quadrados e está contido em \( AB \). O segmento \( EF \), contido em \( AC \), é lado do outro quadrado. Sabendo que \( AG = 4 \, \text{cm} \) e que o lado \( GH \) do quadrado menor mede \( 3 \, \text{cm} \), o comprimento do segmento \( EF \) é:
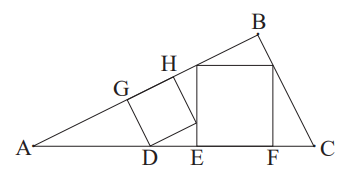
a) \( \frac{121}{20} \) b) \( \frac{111}{20} \) c) \( \frac{102}{15} \) d) \( \frac{98}{15} \)
1º Passo – Calcular \( AD \) no triângulo \( AGD \):
Pelo Teorema de Pitágoras: \[ AD^2 = 3^2 + 4^2 = 9 + 16 = 25 \] \[ AD = 5 \text{ cm} \]
2º Passo – Semelhança de triângulos:
Os ângulos \( \angle GAD \), \( \angle EDJ \) e \( \angle HIJ \) são congruentes, logo, os triângulos \( GAD \), \( EDJ \) e \( HIJ \) são semelhantes.
3º Passo – Cálculo de \( EJ \) pela semelhança:
\[ \frac{3}{EJ} = \frac{5}{9} \implies EJ = \frac{27}{5} \]
4º Passo – Cálculo de \( JI \) pela semelhança:
\[ \frac{4}{3} = \frac{JI}{5} \implies JI = \frac{15}{4} \]
5º Passo – Cálculo de \( EF = EI + EJ + JI \):
\[ EF = \frac{9}{5} + \frac{15}{4} + \frac{36+75}{20} = \frac{111}{20} \text{ cm} \]
Resposta Final: \[ \frac{111}{20} \quad \text{(Alternativa B)} \]
Uma empresa produz arruelas (discos perfurados) pretos no formato indicado na figura a seguir:

O círculo externo tem 60 cm de diâmetro; o interno, 40 cm de diâmetro. Para pintá-las de preto, são adquiridas latas de tinta, sendo que cada lata é suficiente para pintar uma área total de 10 m². Sabendo que somente uma das faces da arruela será pintada, a quantidade mínima de latas que precisarão ser adquiridas para pintar 90 arruelas é:
a) 4 b) 5 c) 6 d) 7
1º Passo – Calcular a área de uma arruela:
O raio do círculo maior é \( R = 30 \) cm = 0,30 m O raio do círculo menor é \( r = 20 \) cm = 0,20 m \[ A = \pi R^2 – \pi r^2 = \pi(0,30^2 – 0,20^2) = 0,05\pi \text{ m²} \]
2º Passo – Calcular a área total de 90 arruelas:
\[ A_{total} = 90 \times 0,05\pi \approx 14,13 \text{ m²} \]
3º Passo – Determinar a quantidade de latas:
Cada lata pinta 10 m², então: \[ \frac{14,13}{10} \approx 1,413 \] Arredondando para cima → **2 latas**.
Observação: Entre as alternativas, 4 é a menor, mas a questão foi **anulada**.
Na figura abaixo, \(ABCD\) representa um terreno quadrado com lados de 10 m, coberto por grama alta. O ponto \(E\) é o ponto médio do lado \(AD\); o segmento \(EF\), paralelo a \(DC\), representa um muro de 5 m de comprimento e 1 m de altura, portanto, intransponível.
Um cortador de grama robótico será usado para cortar a grama do terreno. Ele será ligado na energia no ponto \(A\) e seu cabo de energia tem comprimento de 10 m. Para funcionar, ele precisa estar ligado o tempo todo.
-
a) Ao usar o aparelho para cortar a grama do terreno, uma pessoa tenta se aproximar, ao máximo, do lado \(CD\).
Calcule a distância que falta para o cortador alcançar o lado \(CD\).
b) O robô não conseguirá cortar todo o terreno, pois seu fio é curto e o muro é obstáculo.
Determine a maior área do terreno que o robô conseguirá cortar.
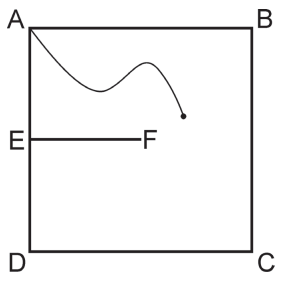
a) Distância faltante para alcançar o lado CD
Primeiro, calculamos \( AF \) no triângulo retângulo: \[ AF^2 = 5^2 + 5^2 \implies AF = 5\sqrt{2} \]
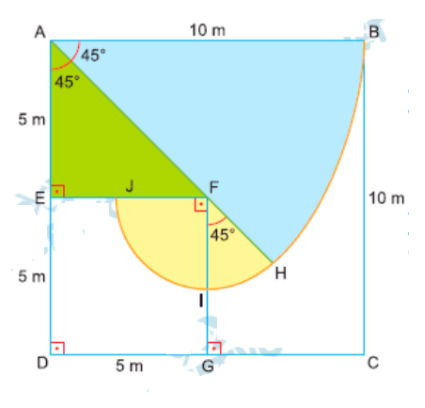
O cabo tem 10 m, logo o ponto mais próximo que o robô chega do lado \(CD\) está a: \[ GI = 5\sqrt{2} – 10 \approx 1 \text{ m de distância} \]
b) Maior área que o robô consegue cortar
A área acessível é composta por setores circulares com raio 10 m, descontando o setor bloqueado pelo muro: \[ A = \frac{45^\circ}{360^\circ} \pi \cdot 10^2 + \frac{135^\circ}{360^\circ} \pi \cdot (10-5\sqrt{2})^2 + 5 \cdot 5 \]
Simplificando: \[ A = \frac{550\pi – 300\pi \sqrt{2} + 100}{8} = \frac{275\pi – 150\pi\sqrt{2} + 50}{4} \text{ m²} \]
Resposta Final: a) \(5\sqrt{2} – 10 \approx 1 \text{ m}\) b) \(\frac{275\pi – 150\pi\sqrt{2} + 50}{4} \text{ m²}\)
No losango abaixo, qual é a medida do segmento \( BE \)?
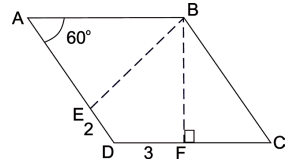
-
a) \(\sqrt{26}\)
b) \(\sqrt{27}\)
c) \(\sqrt{28}\)
d) \(\sqrt{29}\)
1) Determinando o lado do losango:
Pelo triângulo retângulo \( BFC \): \[ \cos 60^\circ = \frac{x-3}{x} \implies \frac{1}{2} = \frac{x-3}{x} \] \[ x = 6 \]
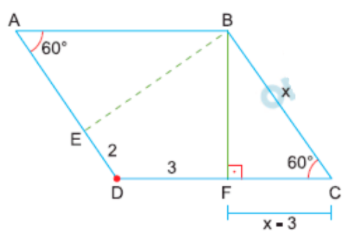
2) Aplicando o Teorema do Cosseno em AEB:
\[ BE^2 = 4^2 + 6^2 – 2 \cdot 4 \cdot 6 \cdot \cos 60^\circ \] \[ BE^2 = 16 + 36 – 24 = 28 \] \[ BE = \sqrt{28} \]
Resposta Final: **Alternativa c) \(\sqrt{28}\)**
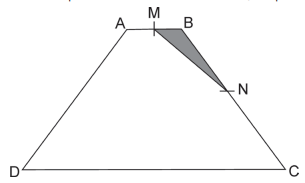
Na figura, \(ABCD\) é um trapézio com \( AB = 1 \) e \( CD = 5 \). Os pontos \( M \) e \( N \) são os pontos médios de \( AB \) e \( BC \), respectivamente.
Sabendo que a área do triângulo \( MBN \) é 1, qual é a área do trapézio \( ABCD \)?
-
a) 18
b) 20
c) 22
d) 24
1) Área do triângulo MBN:
Pela fórmula da área do triângulo: \[ \frac{1}{2} \cdot \frac{1}{2} \cdot h = 1 \implies h = 8 \]
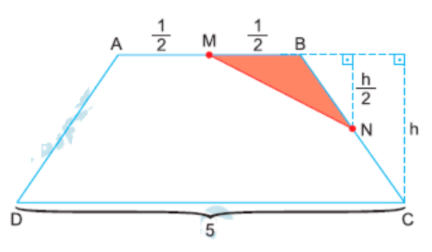
2) Área do trapézio ABCD:
A área de um trapézio é: \[ A = \frac{(B + b) \cdot h}{2} = \frac{(5 + 1) \cdot 8}{2} = 24 \]
Resposta Final: **Alternativa d) 24**
Joaquim estava brincando com um graveto de 50 cm que se quebrou em três pedaços de comprimentos \( a \), \( b \) e \( c \), com \( a \le b \le c \). Ele tentou formar um triângulo com os pedaços, mas não foi possível.
Sabendo que \( b = a+2 \), qual é o maior valor possível de \( a \)?
-
a) 9,5 cm
b) 10,5 cm
c) 11,5 cm
d) 12,5 cm
1) Montando as equações:
\[ a + (a+2) + c = 50 \implies 2a + c = 48 \]
2) Condição para não formar triângulo:
Para que não forme triângulo, o maior lado \( c \) deve ser \[ c \ge a + b = 2a + 2 \]
3) Substituindo \( c = 48-2a \):
\[ 48-2a \ge 2a+2 \implies 46 \ge 4a \implies a \le 11,5 \]
Resposta Final: **Alternativa c) 11,5 cm**
Sr. Gauss tem uma pizzaria, chamada π-zzaria, que vende dois tipos de pizzas circulares: uma individual, de diâmetro \( d \), e uma de 20 cm de diâmetro, partida em quatro pedaços iguais.
Considerando que o preço de uma pizza é proporcional à sua área, qual precisa ser o valor de \( d \) para que quatro pizzas individuais custem o mesmo que uma pizza grande de quatro pedaços?
a) 6 cm b) 8 cm c) 10 cm d) 12 cm
1) Calculando as áreas das pizzas:
Área da pizza grande (diâmetro 20 cm): \[ A = \pi \left(\frac{20}{2}\right)^2 = 100 \pi \]
Área da pizza individual (diâmetro \( d \)): \[ a = \pi \left(\frac{d}{2}\right)^2 = \frac{\pi d^2}{4} \]
2) Igualando o preço proporcional às áreas:
\[ 4 \cdot a = A \] \[ 4 \cdot \frac{\pi d^2}{4} = 100\pi \] \[ \pi d^2 = 100\pi \implies d^2 = 100 \] \[ d = 10 \text{ cm} \]
Resposta Final: Alternativa C — 10 cm
A figura mostra um triângulo retângulo ABC. O ponto \( M \) é o ponto médio do lado \( AB \), que é a hipotenusa.
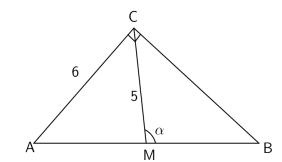
O valor de \( sen \alpha \) é:
-
a) \( \frac{24}{25} \)
b) \( \frac{5}{6} \)
c) \( \frac{1}{2} \)
d) \( \frac{\sqrt{3}}{2} \)
I) Identificando o ponto M:
O ponto \( M \) é o circuncentro do triângulo retângulo \( ABC \), pois é o ponto médio da hipotenusa. Assim, \( AM = BM = CM = 5 \), logo: \[ AB = AM + MB = 5 + 5 = 10 \]
II) Determinando os lados do triângulo:
No triângulo \( ABC \): \[ (BC)^2 + (AC)^2 = (AB)^2 \] \[ (BC)^2 + 6^2 = 10^2 \Rightarrow BC^2 = 64 \Rightarrow BC = 8 \] \[ sen B = \frac{AC}{AB} = \frac{6}{10} = \frac{3}{5} \]
III) Aplicando a lei dos senos no triângulo BMC:
\[ \frac{CM}{sen B} = \frac{BC}{sen \alpha} \] \[ \frac{5}{3/5} = \frac{8}{sen \alpha} \Rightarrow sen \alpha = \frac{24}{25} \]
Resposta Final: Alternativa A.
a) \( b^2 + ac = a^2 + c^2 \)
b) \( a^2 + bc = b^2 + c^2 \)
c) \( a^2 – bc = b^2 + c^2 \)
d) \( b^2 – ac = a^2 + c^2 \)
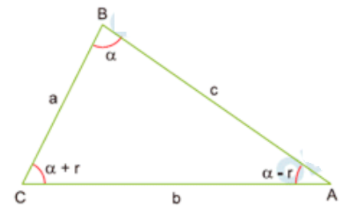
- Seja \( \alpha \) o ângulo médio do triângulo e \( r \) a razão da progressão aritmética dos ângulos.
Então: \[ A = \alpha – r, \quad B = \alpha, \quad C = \alpha + r \] - A soma dos ângulos internos é: \[ (\alpha-r)+\alpha+(\alpha+r)=3\alpha=180^\circ \Rightarrow \alpha=60^\circ \]
- Aplicando a Lei dos Cossenos no triângulo \( ABC \): \[ b^2 = a^2 + c^2 – 2ac \cdot \cos 60^\circ \] \[ b^2 = a^2 + c^2 – ac \] \[ b^2 + ac = a^2 + c^2 \]
- Portanto, a alternativa correta é a **A**.
a) Supondo que \( ABC \) é um triângulo retângulo com perímetro igual a 16 cm e hipotenusa de comprimento 7 cm, calcule sua área.
b) Sabendo que, em um triângulo qualquer, a soma dos comprimentos de quaisquer dois lados é sempre maior que o comprimento do terceiro lado e assumindo que as medidas dos lados de um certo triângulo são \( a \), \( a^2 \) e \( a^3 \), calcule os possíveis valores de \( a \).
a) Área do triângulo retângulo:
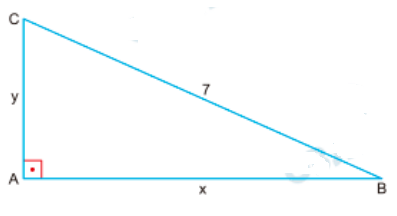
- Sabemos que \( x + y + 7 = 16 \Rightarrow x + y = 9 \).
- Pelo Teorema de Pitágoras: \( x^2 + y^2 = 7^2 = 49 \).
- Usando \( (x+y)^2 = x^2 + 2xy + y^2 = 81 \):
Área \( A = \frac{x \cdot y}{2} = \frac{16}{2} = 8 \text{ cm}^2 \).
b) Lados do triângulo: \( a \), \( a^2 \), \( a^3 \).
- Maior lado < soma dos outros dois:
Para \( 0 < a < 1 \): maior lado é \( a \)
\[ a^3 + a^2 > a \quad \Rightarrow \quad a(a^2 + a – 1) > 0 \]Para \( a > 1 \): maior lado é \( a^3 \)
\[ a^3 < a + a^2 \quad \Rightarrow \quad a^3 - a^2 - a < 0 \]Simplificando, os valores possíveis de \( a \) são:
\[ \frac{-1+\sqrt{5}}{2} < a < 1 \quad \text{ou} \quad 1 < a < \frac{1+\sqrt{5}}{2} \]Resposta final:
- a) \( 8 \text{ cm}^2 \)
- b) \( \frac{-1+\sqrt{5}}{2} < a < 1 \) ou \( 1 < a < \frac{1+\sqrt{5}}{2} \)
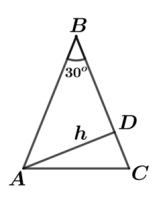
- Identificação do triângulo:
Seja \( \ell = AB = BC \) e \( S \) a área do triângulo \( ABC \). - Usando o triângulo AHB (ângulo de 30°): \[ \sin 30^\circ = \frac{h}{\ell} = \frac{1}{2} \quad \Rightarrow \quad \ell = 2h \]
- Área do triângulo: \[ S = \frac{BC \cdot h}{2} = \frac{2h \cdot h}{2} = h^2 \]
Resposta correta: a) \( h^2 \)
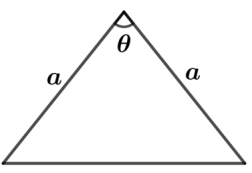
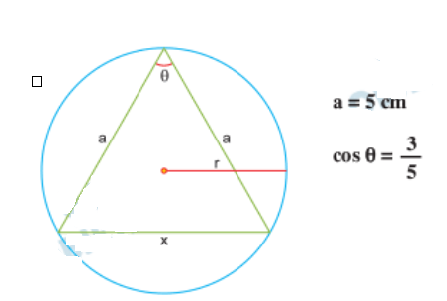
a) Calcule a área desse triângulo.
b) Determine o comprimento do raio da circunferência circunscrita a esse triângulo.
- Calculando o seno de θ:
Sabemos que \( \cos\theta = \frac{3}{5} \). Pela relação fundamental: \[ \sin^2\theta + \cos^2\theta = 1 \] \[ \sin\theta = \frac{4}{5} \] - Área do triângulo: \[ S = \frac{a^2 \cdot \sin\theta}{2} = \frac{5 \cdot 5 \cdot \frac{4}{5}}{2} = 10 \, \text{cm}^2 \]
- Determinando o terceiro lado (x):
Pela lei dos cossenos: \[ x^2 = a^2 + a^2 – 2a^2\cos\theta \] \[ x^2 = 50 – 30 = 20 \quad \Rightarrow \quad x = 2\sqrt{5} \] - Determinando o raio da circunferência circunscrita (R):
Fórmula da área usando o raio: \[ S = \frac{a \cdot a \cdot x}{4R} \] \[ 10 = \frac{5 \cdot 5 \cdot 2\sqrt{5}}{4R} \quad \Rightarrow \quad R = \frac{5\sqrt{5}}{4} \, \text{cm} \] - a) \( 10 \, \text{cm}^2 \)
- b) \( \frac{5\sqrt{5}}{4} \, \text{cm} \)
Respostas:
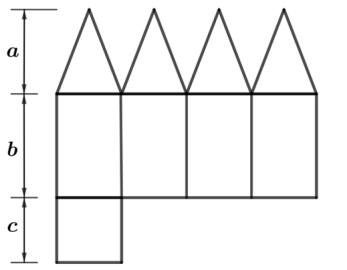
a) Determine o número de vértices e de arestas desse poliedro.
b) Para \(a = 13 \text{ cm}\), \(b = 16 \text{ cm}\) e \(c = 10 \text{ cm}\), calcule o volume desse poliedro.
- Identificação do poliedro:
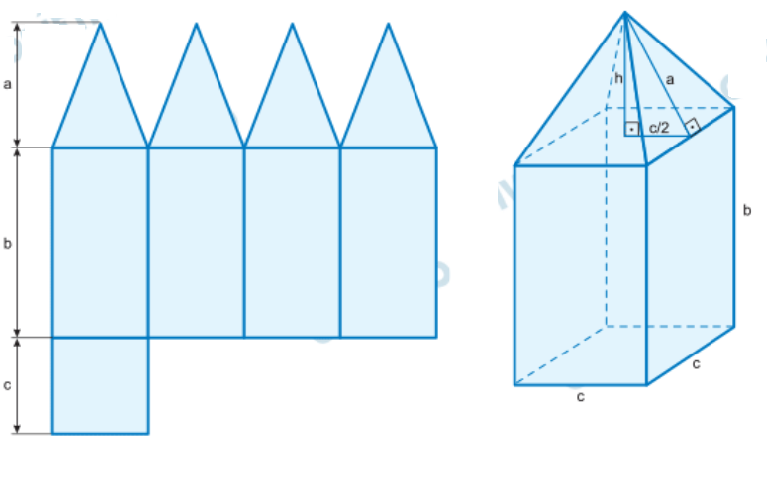
O poliedro é formado por uma pirâmide reta sobre um paralelepípedo reto-retângulo.
– Base da pirâmide: quadrado de lado \(c\) – Altura da face lateral da pirâmide: \(a\) – Base do paralelepípedo: quadrado de lado \(c\) – Altura do paralelepípedo: \(b\)
Logo, o poliedro possui **9 vértices e 16 arestas**.- Cálculo do volume:
Primeiro, calculamos a altura \(h\) da pirâmide usando Pitágoras: \[ a^2 = h^2 + \left(\frac{c}{2}\right)^2 \quad \Rightarrow \quad 13^2 = h^2 + 5^2 \quad \Rightarrow \quad h = 12 \text{ cm} \] O volume do poliedro é a soma do volume da pirâmide e do paralelepípedo: \[ V = \frac{1}{3} c^2 h + c^2 b \] \[ V = \frac{1}{3} \cdot 10^2 \cdot 12 + 10^2 \cdot 16 = 2000 \text{ cm}^3 \]Respostas:
- a) 9 vértices e 16 arestas
- b) \(2000 \text{ cm}^3\)
- Cálculo do volume:
6. Dicas de Estudo e Preparação
Para maximizar seu aprendizado e desempenho em geometria plana Unicamp vestibular, siga estas recomendações:
- Resolva provas anteriores da UNICAMP, principalmente das edições 2020 a 2025, com foco nas questões geométricas.
- Pratique exercícios com figuras compostas e desconstruídas, envolvendo setores de círculo, sobreposição de polígonos e triângulos inscritos.
- Estude semelhança e proporção de modo sistemático: observe como a banca explora razão entre áreas como tema central.
- Intercale estudos teóricos com simulados cronometrados, garantindo tempo realista por questão.
- Use ferramentas gráficas (geogebra ou papel milimetrado) para desenhar e validar visualmente os êxitos.
- Reforce conexões com geometria analítica e trigonometria, já que a UNICAMP frequentemente mistura temas para aumentar o grau de abstração.
Leia também
O que Cai em Matemática na UNICAMP – Guia Completo para o Vestibular
Preparação UNICAMP- Todas as Provas Anteriores
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:
7. Conclusão
A geometria plana Unicamp vestibular se mantém como um conteúdo estratégico, com 13 questões entre 2020 e 2025, representando mais de 10% da prova de matemática. Sua frequência e peso exigem que o candidato domine não apenas teoria, mas saiba aplicar conceitos com precisão e clareza. Estudar de forma orientada e prática — resolvendo provas anteriores e treinando em contextos reais — é essencial para conquistar uma boa nota.
Domine os triângulos, polígonos, circunferências e construções auxiliares, desenvolva um raciocínio geométrico visual e eficiente — e você estará muito bem preparado para vencer essa área crítica da prova da UNICAMP.






















