Gráfico da Função Cosseno
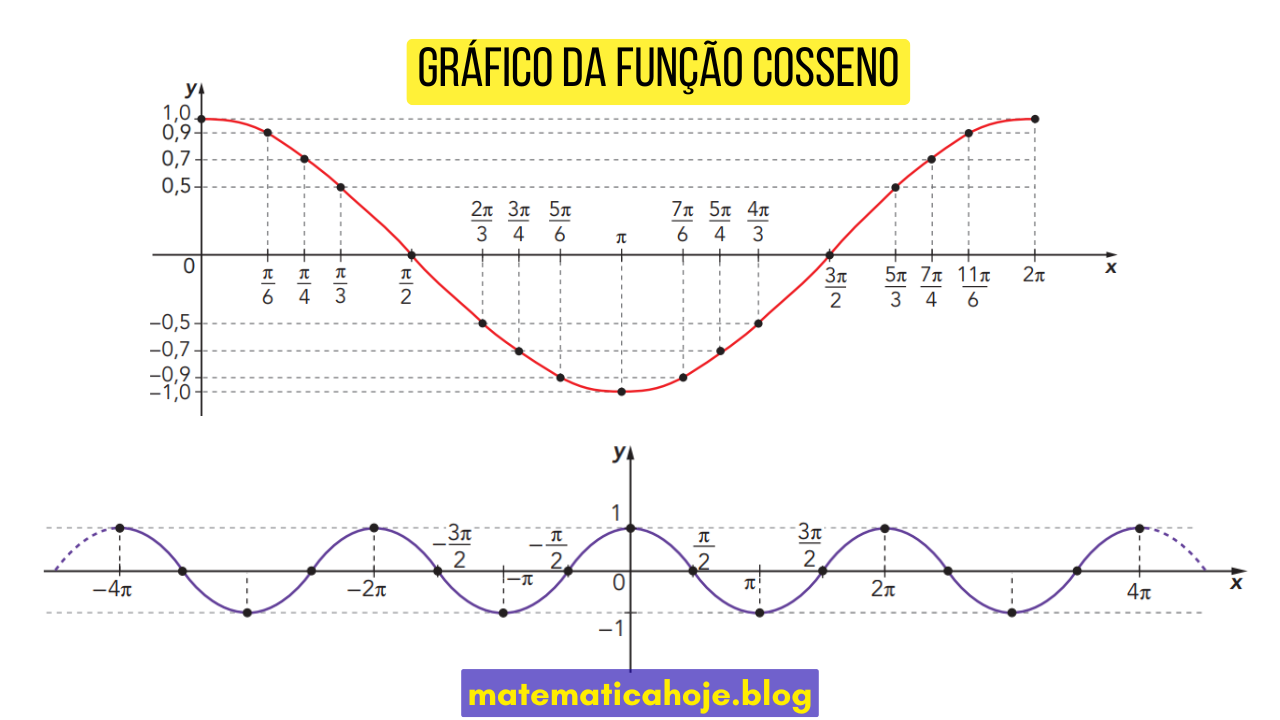
A função cosseno, representada por \(f(x)=\cos x\), é uma das funções trigonométricas mais estudadas. Seu gráfico apresenta uma forma ondulatória que se repete indefinidamente, oscilando entre \(-1\) e \(1\).
• A função é periódica com período \(2\pi\).
• Possui máximos em \(f(x)=1\) e mínimos em \(f(x)=-1\).
• É uma função par: \(\cos(-x)=\cos(x)\).
Pontos Notáveis
No intervalo \([0,2\pi]\), destacam-se:
- \(\cos(0)=1\)
- \(\cos(\pi/2)=0\)
- \(\cos(\pi)=-1\)
- \(\cos(3\pi/2)=0\)
- \(\cos(2\pi)=1\)
Características do Gráfico
- Domínio: todos os números reais (\(\mathbb{R}\)).
- Imagem: valores em \([-1,1]\).
- Simetria: gráfico simétrico em relação ao eixo \(y\).
- Amplitude: 1 (distância do eixo até o valor máximo).
Exemplo Resolvido
Exemplo: Calcule \(\cos(330^\circ)\).
Solução:
\(330^\circ=360^\circ-30^\circ\)
\(\cos(330^\circ)=\cos(30^\circ)=\dfrac{\sqrt{3}}{2}\).
Resposta final: \(\dfrac{\sqrt{3}}{2}\).
Exercícios de Múltipla Escolha
1) O valor de \(\cos(\pi)\) é:
A) 1
B) 0
C) -1
D) \(\dfrac{\sqrt{3}}{2}\)
Ver solução
\(\cos(\pi)=-1\). Resposta: C.
2) Qual o período da função \(y=\cos x\)?
A) \(\pi\)
B) \(2\pi\)
C) \(4\pi\)
D) \(\dfrac{\pi}{2}\)
Ver solução
O gráfico repete a cada \(2\pi\). Resposta: B.
3) A função \(y=\cos x\) é:
A) Ímpar
B) Par
C) Constante
D) Não possui simetria
Ver solução
Como \(\cos(-x)=\cos(x)\), a função é par. Resposta: B.






















