Gráfico da Função Exponencial
Interprete e construa gráficos exponenciais: casos crescente e decrescente, propriedades e exercícios.
A função exponencial padrão é
Domínio: \(\mathbb{R}\)
Imagem: \((0,+\infty)\)
Ponto comum: \((0,1)\) pois \(a^{0}=1\)
Assíntota horizontal: eixo \(x\) (reta \(y=0\))
\[ f(x)=a^{x} \quad (a>0,\; a\neq 1) \]
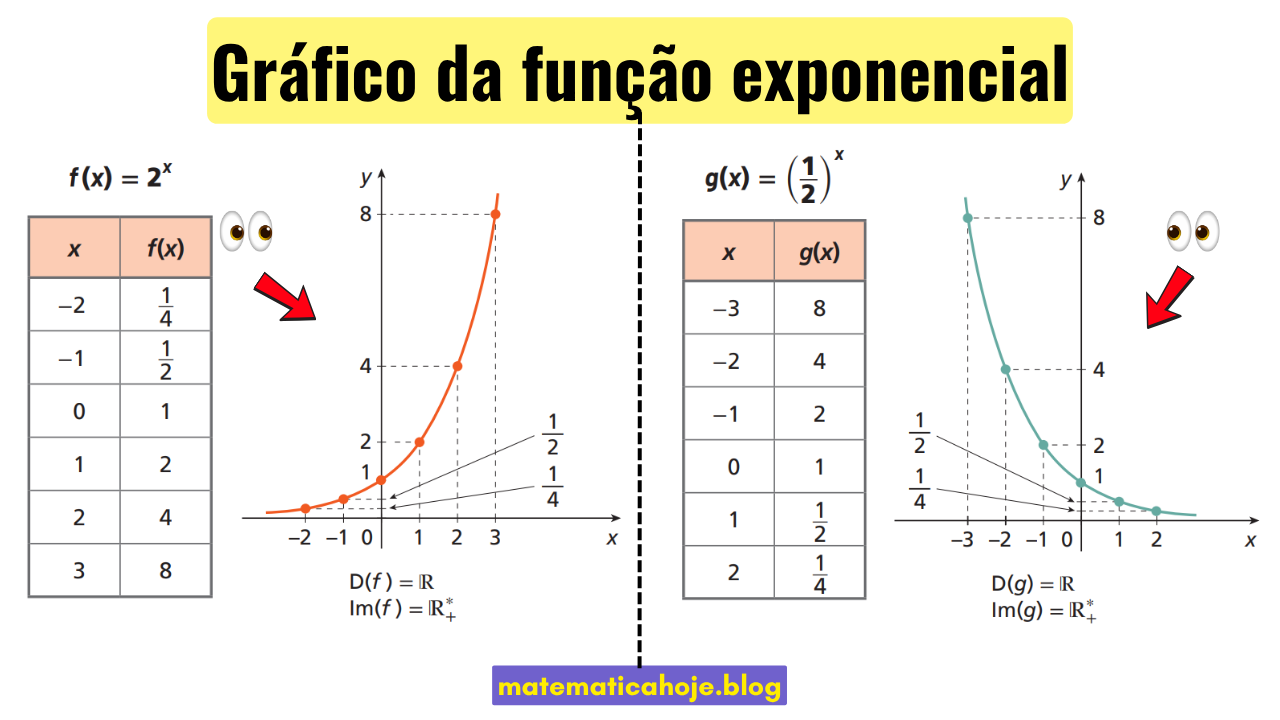
O gráfico muda conforme a base: crescente se \(a>1\) e decrescente se \(01) Caso crescente — \(f(x)=2^{x}\)
Tabela de valores
| x | f(x) |
|---|---|
| -2 | \(\tfrac14\) |
| -1 | \(\tfrac12\) |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
O gráfico cresce rapidamente para a direita e se aproxima de \(y=0\) para a esquerda.
2) Caso decrescente — \(g(x)=\left(\tfrac12\right)^{x}\)
Tabela de valores
| x | g(x) |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | \(\tfrac12\) |
| 2 | \(\tfrac14\) |
O gráfico exibe decaimento rápido à direita do eixo \(y\) e aproxima-se de \(y=0\) quando \(x\to+\infty\).
📘 Quer um resumo pronto para consulta?
Baixe grátis o eBook Fórmulas Matemática
Baixe grátis o eBook Fórmulas Matemática
3) Exercícios de múltipla escolha
(1) O gráfico de \(h(x)=3^{x}\) passa obrigatoriamente por qual ponto?
- A) \((1,0)\)
- B) \((0,1)\)
- C) \((3,0)\)
- D) \((0,3)\)
Para toda exponencial \(a^{x}\), \(h(0)=1\).
Resposta correta: B) \((0,1)\).
(2) Para \(p(x)=\left(\tfrac14\right)^x\), podemos afirmar que o gráfico é:
- A) Crescente
- B) Decrescente
- C) Constante
- D) Linear
Como \(0Resposta correta: B.
(3) Em \(f(x)=2^{x}\), o valor de \(f(-3)\) é:
- A) \(8\)
- B) \(\tfrac{1}{8}\)
- C) \(\tfrac{1}{3}\)
- D) \(0\)
\(2^{-3}=\tfrac{1}{2^{3}}=\tfrac{1}{8}\).
Resposta correta: B.