📈 Gráfico da Função Seno
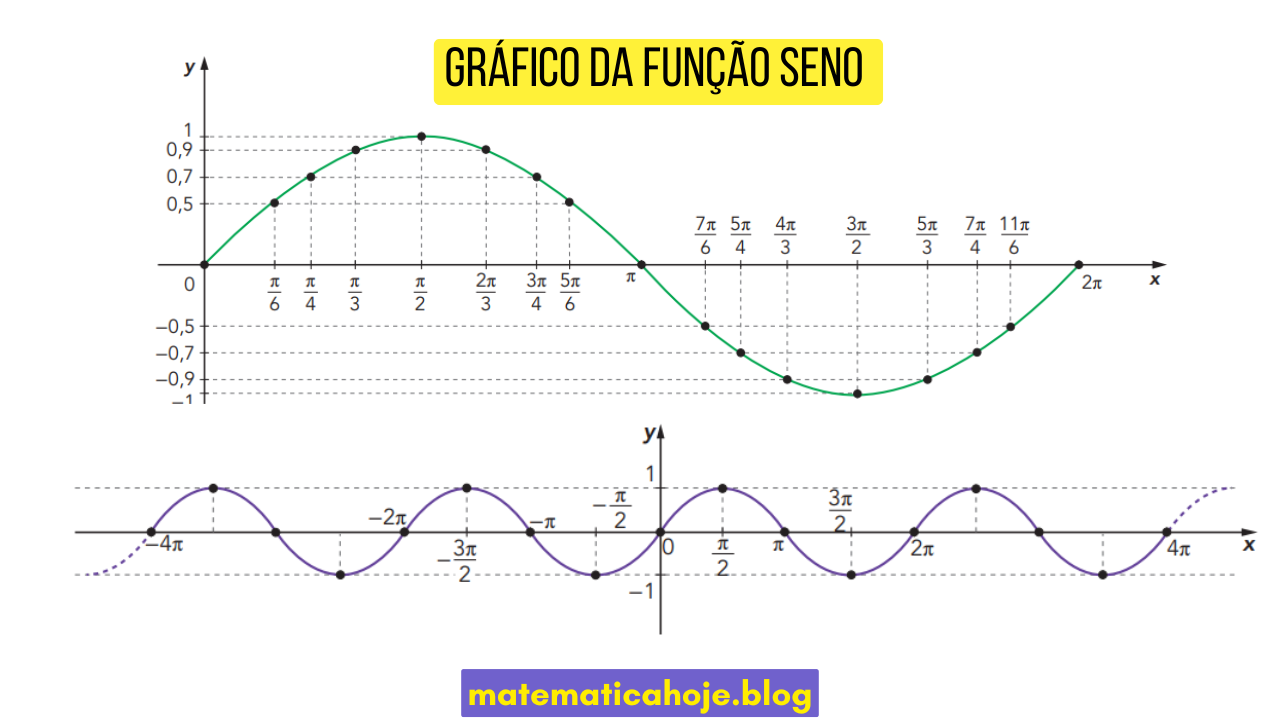
O gráfico de \(y = sen x\) é uma curva suave e ondulatória, que aparece em fenômenos naturais como ondas, movimentos circulares e vibrações periódicas. Ele é fundamental para o estudo da trigonometria e da análise de funções periódicas.
• Amplitude: 1
• Período: 2π
• Valores entre: [-1, 1]
• Função ímpar (simétrica em relação à origem).
📌 Pontos Notáveis
- Interceptos no eixo \(x\): \(x = k\pi\) (onde \(k \in \mathbb{Z}\)).
- Máximos: \(y=1\) em \(x=\frac{\pi}{2}+2k\pi\).
- Mínimos: \(y=-1\) em \(x=\frac{3\pi}{2}+2k\pi\).
🔢 Valores Clássicos
\(sen 0 = 0\)
\(sen \tfrac{\pi}{6} = \tfrac{1}{2}\)
\(sen \tfrac{\pi}{4} = \tfrac{\sqrt{2}}{2}\)
\(sen \tfrac{\pi}{3} = \tfrac{\sqrt{3}}{2}\)
\(sen \tfrac{\pi}{2} = 1\)
\(sen \pi = 0\)
\(sen \tfrac{3\pi}{2} = -1\)
\(sen 2\pi = 0\)
\(sen(-x) = -sen x\) (ímpar)
\(sen(x+\pi) = -sen x\) (antiperiódica)
📊 Simetria e Monotonia
- Função ímpar: simétrica em relação à origem.
- Crescente: de \(-\tfrac{\pi}{2}\) até \(\tfrac{\pi}{2}\).
- Decrescente: de \(\tfrac{\pi}{2}\) até \(\tfrac{3\pi}{2}\).
⚙️ Transformações Gerais
A função transformada é:
\(y = a \cdot sen(bx + c) + d\)
- Amplitude: \(|a|\).
- Período: \(T = \tfrac{2\pi}{|b|}\).
- Deslocamento horizontal: \(-\tfrac{c}{b}\).
- Deslocamento vertical: \(d\).
📘 Exemplo Resolvido
Considere \(y = 2sen(3x – \tfrac{\pi}{3}) – 1\).
- Amplitude: 2
- Período: \(\tfrac{2\pi}{3}\)
- Deslocamento horizontal: \(\tfrac{\pi}{9}\)
- Deslocamento vertical: \(-1\)
O gráfico será uma onda de altura 2, repetindo-se a cada \(\tfrac{2\pi}{3}\), deslocada para a direita e para baixo.
📝 Exercícios de Múltipla Escolha
1) O período da função \(y = sen x\) é:
A) \(\pi\)
B) \(2\pi\)
C) \(\tfrac{\pi}{2}\)
D) \(4\pi\)
Ver solução
O seno repete seu comportamento a cada \(2\pi\). Resposta: B.
2) Qual o valor de \(sen \tfrac{3\pi}{2}\)?
A) \(1\)
B) \(-1\)
C) \(0\)
D) \(\tfrac{\sqrt{3}}{2}\)
Ver solução
Em \(\tfrac{3\pi}{2}\) o gráfico atinge o mínimo: \(y=-1\). Resposta: B.
3) A função \(y = 3sen x\) possui amplitude:
A) 1
B) 2
C) 3
D) 6
Ver solução
A amplitude é o valor absoluto do coeficiente \(a\). Logo, amplitude = 3. Resposta: C.





















