Gráfico: Domínio e Imagem
Como ler intervalos diretamente do gráfico — com exemplos, armadilhas e exercícios resolvidos.
Este guia mostra como extrair domínio (todos os valores de \(x\) usados) e imagem (todos os \(y\) produzidos) olhando apenas para o gráfico. Antes, vale revisar: Plano Cartesiano, Gráfico de uma Função, Domínio de uma Função, Imagem de uma Função e Contradomínio. Para treinar, use o Banco de Questões.
- Domínio \(D(f)\): conjunto de todas as abscissas \(x\) para as quais \(f(x)\) está definido (procure a “sombra” do traço no eixo \(x\)).
- Imagem \(\mathrm{Im}(f)\): conjunto de todos os valores \(y=f(x)\) que aparecem (a “sombra” no eixo \(y\)).
Como ler no gráfico — passo a passo
- Varra horizontalmente o desenho e projete no eixo \(x\): isso dá o domínio.
- Varra verticalmente e projete no eixo \(y\): isso dá a imagem.
- Círculo fechado = ponto incluído; círculo aberto = ponto excluído.
- Se houver “buracos” ou interrupções, escreva o resultado como união de intervalos.
- Setas na ponta indicam que o gráfico continua e o intervalo é infinito.
Notação de intervalos (lembrete rápido)
| Notação | Leitura | Inclui extremidades? |
|---|---|---|
| \([a,b]\) | entre \(a\) e \(b\) | sim, sim |
| \((a,b)\) | entre \(a\) e \(b\) | não, não |
| \([a,b)\) | de \(a\) até \(b\) | sim, não |
| \((-\infty,b]\) | menores ou iguais a \(b\) | ∞ nunca é incluído |
| \([a,\infty)\) | maiores ou iguais a \(a\) | ∞ nunca é incluído |
Exemplo guiado usando a figura
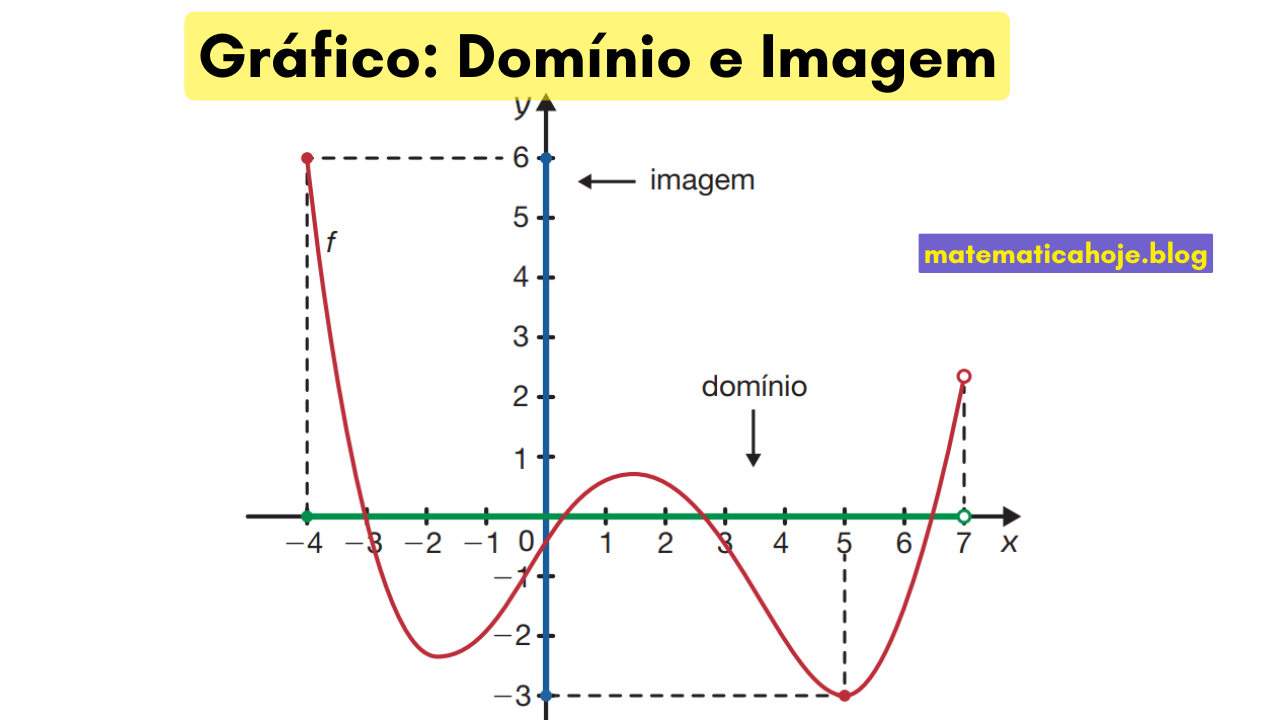
No gráfico acima, observamos:
- O traço começa em \(x=-4\) com ponto fechado e termina em \(x=7\) com ponto aberto ⇒ domínio \(\;D(f)=[-4,\,7)\).
- O menor valor de \(y\) é \(-3\) (ponto fechado) e o maior é \(6\) (atingido) ⇒ imagem \(\;\mathrm{Im}(f)=[-3,\,6]\).
Armadilhas comuns
- Buracos (círculo aberto): o valor não pertence ao conjunto correspondente.
- Domínio ≠ contradomínio: o contradomínio é o conjunto-alvo declarado; a imagem é o que de fato aparece no gráfico.
- Função “por partes”: pode gerar união de intervalos no domínio e “saltos” na imagem.
- Escalas diferentes: confira as marcações dos eixos antes de ler valores.
Exercícios (múltipla escolha) com solução
1) Pelo gráfico desta página, assinale o par correto \((D(f),\mathrm{Im}(f))\):
- \(([-4,7),\,[-3,6])\)
- \(((-4,7],\,(-3,6))\)
- \(([-4,7],\,[-3,6))\)
- \(((-4,7),\,[-3,6])\)
Ver solução
2) Para \(g(x)= (x-5)^2-3\) com domínio \(\mathbb{R}\), a imagem é:
- \((-\infty,-3]\)
- \([-3,\infty)\)
- \((-\infty,\infty)\)
- \([-5,3]\)
Ver solução
3) Para \(h(x)=|x-2|\) restrita a \(x\ge0\), temos:
- \(D(h)=[0,\infty)\) e \(\mathrm{Im}(h)=[0,\infty)\)
- \(D(h)=(-\infty,\infty)\) e \(\mathrm{Im}(h)=[0,\infty)\)
- \(D(h)=[0,\infty)\) e \(\mathrm{Im}(h)=(-\infty,\infty)\)
- \(D(h)=(0,\infty)\) e \(\mathrm{Im}(h)=(0,\infty)\)
Ver solução
4) A função \(p(x)=\dfrac{x^2-1}{x-1}\) tem:
- \(D=\mathbb{R}\) e \(\mathrm{Im}=\mathbb{R}\)
- \(D=\mathbb{R}\setminus\{1\}\) e \(\mathrm{Im}=\mathbb{R}\)
- \(D=\mathbb{R}\setminus\{1\}\) e \(\mathrm{Im}=\mathbb{R}\setminus\{2\}\)
- \(D=\mathbb{R}\) e \(\mathrm{Im}=\mathbb{R}\setminus\{2\}\)
Ver solução
5) Considere \(q(x)=2x+3\) com \(x\in[-1,3]\). O par \((D(q),\mathrm{Im}(q))\) é:
- \(([-1,3],[1,9])\)
- \(([-1,3],[-1,3])\)
- \(((-1,3),(1,9))\)
- \(((-1,3],[1,9))\)
Ver solução
6) O gráfico de uma função possui setas nas duas pontas e um mínimo global em \(y=-2\). A imagem é:
- \((-\infty,-2]\)
- \([-2,\infty)\)
- \((-\infty,\infty)\)
- \([-2,2]\)
Ver solução
Continue estudando (links internos)
• Plano Cartesiano
• Gráfico de uma Função
• Domínio de uma Função
• Imagem de uma Função
• ENEM Matemática
• Coleção 10 eBooks de Matemática





















