Icosaedro (regular)
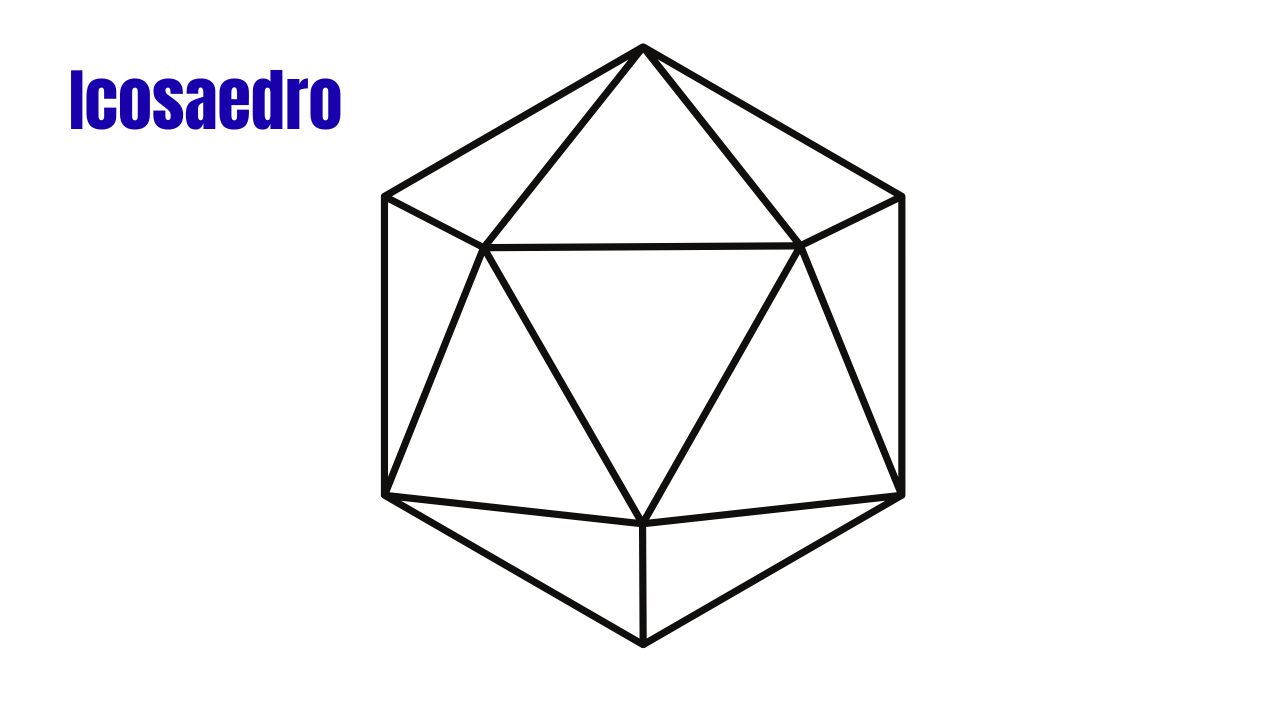
O icosaedro regular é um dos cinco Sólidos de Platão. É composto por 20 faces em forma de triângulos equiláteros, 30 arestas e 12 vértices. Esses números satisfazem a relação de Euler \(V-E+F=2\): \(12-30+20=2\).
Símbolos que usaremos
- \(a\) — comprimento da aresta (lado do triângulo equilátero).
- \(A_t\) — área total da superfície.
- \(V\) — volume.
- \(R\) — raio da esfera circunscrita (centro → vértice).
- \(r\) — raio da esfera inscrita (centro → plano de face).
- \(\varphi\) — número de ouro: \(\displaystyle \varphi=\frac{1+\sqrt5}{2}\approx1{,}618\).
Fórmulas do icosaedro regular
Área total (20 triângulos equiláteros):
\[ A_t = 20\cdot\frac{\sqrt3}{4}a^2 = \boxed{\,5\sqrt3\,a^2\,}. \]
Volume:
\[ \boxed{\,V=\frac{5}{12}(3+\sqrt5)\,a^3\,} \;\; \approx 2{,}1817\,a^3. \]
Raios (esferas notáveis):
\[ \boxed{\,R=\frac{a}{4}\sqrt{\,10+2\sqrt5\,}\,}, \qquad \boxed{\,r=\frac{a}{12}\sqrt3\,(3+\sqrt5)\,}. \]
Ângulo diedro entre faces:
\[ \cos\delta = -\frac{\sqrt5}{3} \quad \Rightarrow \quad \delta \approx 138{,}19^\circ. \]
De onde vêm essas fórmulas?
- Área total: cada face é um triângulo equilátero de área \((\sqrt3/4)a^2\). Como são 20 faces, \(A_t=20(\sqrt3/4)a^2\).
- Volume: pode-se decompor o icosaedro em 20 pirâmides congruentes (vértice no centro, base em cada face), somando \(V=20\cdot(1/3)\cdot A_\triangle \cdot r\).
- R e r: resultam de relações geométricas com o número de ouro em um sistema de coordenadas para o icosaedro (veja abaixo “Coordenadas”).
Coordenadas canônicas (com número de ouro)
Um conjunto de vértices para um icosaedro centrado na origem é dado, até um fator de escala, por: \[ (0,\pm1,\pm\varphi),\quad (\pm1,\pm\varphi,0),\quad (\pm\varphi,0,\pm1). \] Para obter uma aresta de comprimento \(a\), basta escalar todas as coordenadas por um fator adequado (o que é equivalente a multiplicar tudo por \(a\) dividido pelo comprimento da aresta do conjunto padrão).
Exemplo numérico
Considere um icosaedro regular com aresta \(a=6\) cm.
| Grandeza | Cálculo | Valor aproximado |
|---|---|---|
| Área total \(A_t\) | \(5\sqrt3\,a^2 = 5\sqrt3\cdot36\) | \(\approx \mathbf{311{,}76\ \text{cm}^2}\) |
| Volume \(V\) | \(\dfrac{5}{12}(3+\sqrt5)\cdot 216\) | \(\approx \mathbf{471{,}32\ \text{cm}^3}\) |
| Raio circunscrito \(R\) | \(\dfrac{a}{4}\sqrt{10+2\sqrt5}\) | \(\approx \mathbf{5{,}71\ \text{cm}}\) |
| Raio inscrito \(r\) | \(\dfrac{a}{12}\sqrt3\,(3+\sqrt5)\) | \(\approx \mathbf{4{,}54\ \text{cm}}\) |
Use \(\sqrt5\approx2{,}236\) e \(\sqrt3\approx1{,}732\) quando precisar.
Planificação e construção
A planificação (net) mais direta do icosaedro usa 20 triângulos equiláteros (lado \(a\)) organizados em tiras. Para montar:
- Recorte os triângulos e marque as linhas de dobra (tracejado) com um leve vinco.
- Monte uma “cinta” fechada e, em seguida, vá fechando os topos com triângulos restantes.
- Use papel 180–240 g/m² e abas estreitas (5–8 mm) para colagem mais limpa.
Aplicações e onde aparece
- Geodésicas e domos: subdividindo faces do icosaedro obtêm-se esferas geodésicas para estádios e planetários.
- Química/biologia: muitos capsídeos virais têm simetria icosaédrica.
- Design/jogos: o dado de 20 faces (d20) é icosaédrico.
- Truncamentos: o icosaedro truncado leva ao famoso poliedro do “bolão de futebol”.
Veja também
- Sólidos de Platão – panorama dos cinco sólidos regulares.
- Dodecaedro – dual do icosaedro: vértices ↔ faces.
- Octaedro • Hexaedro (cubo) • Tetraedro regular
- Exercício Octaedro e Exercício Dodecaedro – listas modelo com soluções.
Resumo rápido
- \(F=20\), \(E=30\), \(V=12\) • Euler ok.
- \(A_t=5\sqrt3\,a^2\) • \(V=\frac{5}{12}(3+\sqrt5)a^3\).
- \(R=\dfrac{a}{4}\sqrt{10+2\sqrt5}\) • \(r=\dfrac{a}{12}\sqrt3\,(3+\sqrt5)\).
- Diedro \(\delta\approx 138{,}19^\circ\) (\(\cos\delta=-\sqrt5/3\)).
- Cheio de conexões com o número de ouro \(\varphi\).






















