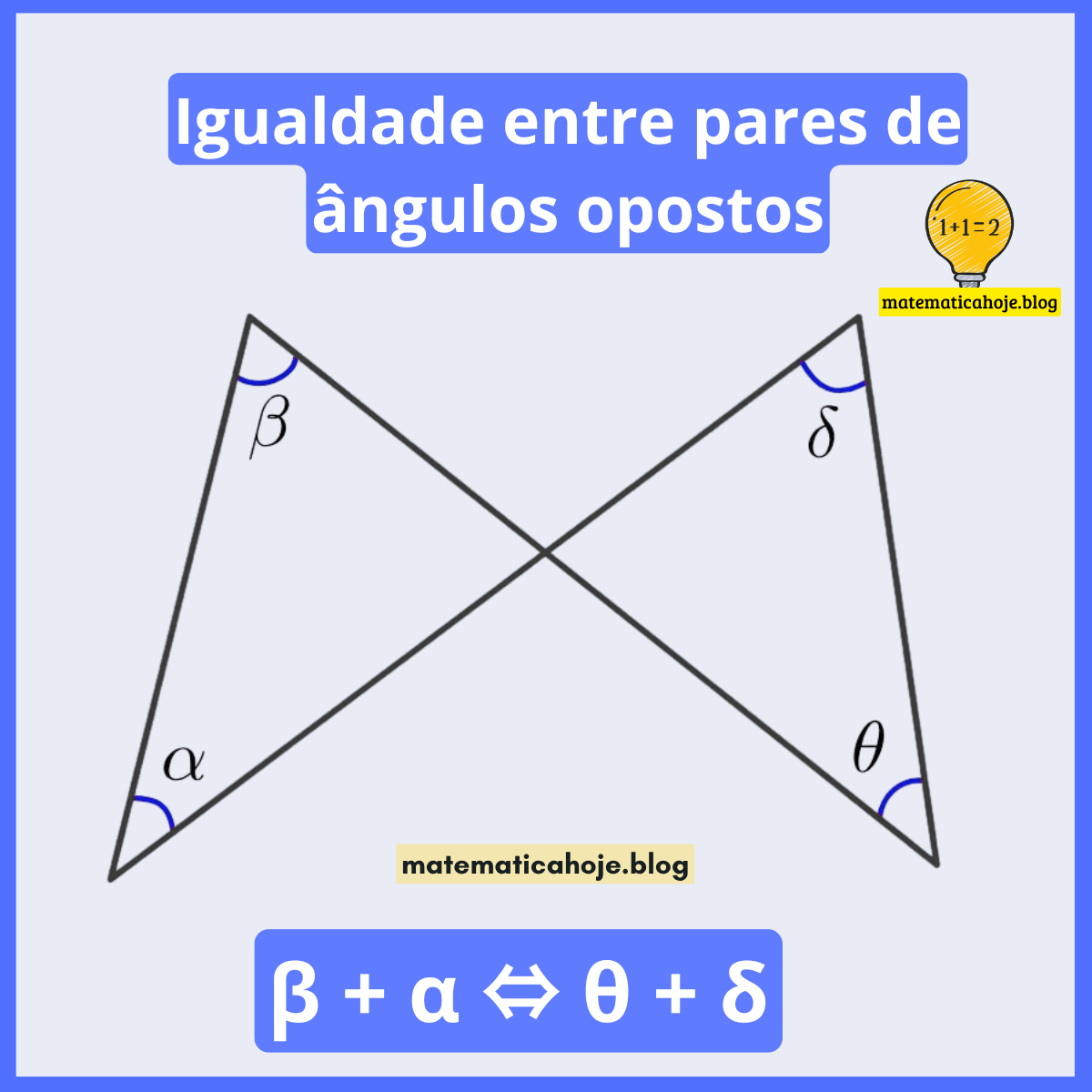
Igualdade entre pares de ângulos opostos — \( \beta + \alpha = \theta + \delta \)

Quando duas retas se cruzam formando uma configuração em “X”, aparecem dois triângulos opostos por um vértice. Nessa situação, a soma dos ângulos dos vértices externos de um triângulo é igual à soma dos ângulos correspondentes do outro.

Teorema: Se duas retas secantes formam dois triângulos opostos por um vértice, então \( \alpha + \beta = \theta + \delta \).

Conexões úteis: Soma dos Ângulos Internos, Soma dos Ângulos Externos e Teorema do Ângulo Externo.

Configuração em X com dois triângulos opostos: β + α = θ + δ — Imagem: matematicaoje.blog — em triângulos opostos por um vértice, \( \beta + \alpha = \theta + \delta \).

Prova em 3 linhas (com a soma dos internos)

Seja \( \varphi \) o ângulo no ponto de interseção das retas. Os ângulos do cruzamento são opostos pelo vértice, então são iguais.

No triângulo da esquerda: \( \alpha + \beta + \varphi = 180^\circ \)
No triângulo da direita: \( \theta + \delta + \varphi = 180^\circ \)
Subtraindo as igualdades: \( \alpha + \beta = \theta + \delta \)

Moral: as somas dos “ângulos das pontas” dos dois triângulos são iguais porque ambos “completam” o mesmo \( \varphi \) até \(180^\circ\).

Mapas Mentais de Matemática — Destaque

Revisão visual de triângulos, ângulos, semelhança e também matemática básica (operações com números inteiros, regras de sinais, adição e subtração de inteiros, multiplicação e divisão com sinais — “jogo de sinais”).

Quero estudar com Mapas Mentais

Exemplos resolvidos (passo a passo)

Exemplo 1 — Encontrar uma soma de ângulos

Na figura em “X”, \( \varphi = 62^\circ \). Sabendo que no triângulo da esquerda \( \alpha = 31^\circ \), calcule \( \beta \) e a soma \( \alpha + \beta \). Depois compare com \( \theta + \delta \).

Ver solução

Triângulo esquerdo: \( \alpha + \beta + \varphi = 180^\circ \)
\(31^\circ + \beta + 62^\circ = 180^\circ\)
\(\beta + 93^\circ = 180^\circ\)
\(\beta = 180^\circ – 93^\circ\)
\(\beta = 87^\circ\)
\(\alpha + \beta = 31^\circ + 87^\circ\)
\(\alpha + \beta = 118^\circ\)
No triângulo direito: \( \theta + \delta + \varphi = 180^\circ \Rightarrow \theta + \delta = 180^\circ – 62^\circ = 118^\circ\)
Logo, \( \alpha + \beta = \theta + \delta = 118^\circ \)

Exemplo 2 — Determinar um ângulo do outro triângulo

Dado \( \alpha = 40^\circ \), \( \beta = 53^\circ \) e \( \delta = 70^\circ \). Calcule \( \theta \).

Ver solução

Pelo teorema: \( \alpha + \beta = \theta + \delta \)
\(40^\circ + 53^\circ = \theta + 70^\circ\)
\(93^\circ = \theta + 70^\circ\)
\(\theta = 93^\circ – 70^\circ\)
\(\theta = 23^\circ\)

Exemplo 3 — Com incógnitas algébricas

Se \( \alpha = 2x + 5^\circ \), \( \beta = x + 10^\circ \) e \( \delta = 3x – 1^\circ \), determine \( \theta \).

Ver solução

\( \alpha + \beta = \theta + \delta \)
\((2x+5^\circ) + (x+10^\circ) = \theta + (3x-1^\circ)\)
\(3x + 15^\circ = \theta + 3x – 1^\circ\)
\(\theta = 3x + 15^\circ – 3x + 1^\circ\)
\(\theta = 16^\circ\)

eBook Gratuito de Fórmulas Matemáticas — Destaque

Tabelas de ângulos, polígonos, semelhança e um reforço de matemática básica (operações com números inteiros, regras de sinais: adição e subtração de inteiros, multiplicação e divisão com sinais).

Baixar grátis agora

Exercícios propostos (com toggle)

Escreva as contas uma abaixo da outra após o “=” para leitura perfeita no celular.

1) Discursiva — Placas cruzadas

Em duas placas que se cruzam, \( \alpha = 28^\circ \) e \( \delta = 77^\circ \). Sabendo que \( \alpha + \beta = \theta + \delta \), determine \( \theta – \beta \).

Ver solução

\(\alpha + \beta = \theta + \delta\)
\(28^\circ + \beta = \theta + 77^\circ\)
\(\theta – \beta = 28^\circ – 77^\circ\)
\(\theta – \beta = -49^\circ\)

2) Múltipla escolha — Somas iguais

Na figura, \( \alpha = 36^\circ \), \( \beta = 44^\circ \) e \( \theta = 70^\circ \). Quanto vale \( \delta \)?

\(32^\circ\)
\(40^\circ\)
\(46^\circ\)
\(50^\circ\)

Mostrar alternativa correta

\(\alpha + \beta = \theta + \delta\) \(36^\circ + 44^\circ = 70^\circ + \delta\) \(80^\circ = 70^\circ + \delta\) \(\delta = 10^\circ\)

Gabarito: nenhuma das alternativas (ajuste o item A para 10° ou atualize o enunciado).

3) Discursiva — Descubra o ângulo do outro triângulo

Se \( \alpha = 2y \), \( \beta = 3y \) e \( \theta = 80^\circ \), encontre \( \delta \).

Ver solução

\(\alpha + \beta = \theta + \delta\)
\(2y + 3y = 80^\circ + \delta\)
\(5y = 80^\circ + \delta\)
Sem mais dados não achamos \(y\) nem \(\delta\) separadamente.
Se o problema disser \(y = 18^\circ\):
\(5y = 90^\circ = 80^\circ + \delta\)
\(\delta = 10^\circ\)

Links internos e produtos do blog

Soma dos Ângulos Internos — base para a prova Soma dos Ângulos Externos — giro total de 360° Teorema do Ângulo Externo — \( \theta = \alpha + \beta \) ENEM Matemática — trilhas, listas e simulados 10 eBooks de Matemática — pacote completo Banco de Questões de Matemática — itens editáveis Mapas Mentais de Matemática — revisão visual rápida eBook Gratuito de Fórmulas Matemáticas — baixe agora

Conclusão

Na configuração em “X”, os triângulos opostos por um vértice compartilham o ângulo do cruzamento. Por isso, as somatórias dos ângulos das pontas são iguais: \( \beta + \alpha = \theta + \delta \). Combine esse fato com a soma dos internos, a soma dos externos e o teorema do ângulo externo para resolver questões com rapidez.

Próximo passo: baixe o eBook gratuito de Fórmulas e siga a rota de estudos no ENEM Matemática.