Imagem da Função Quadrática: como encontrar (com exemplos passo a passo)
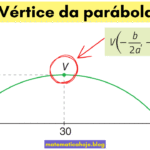
A imagem — também chamada de conjunto-imagem — de uma função quadrática \(f(x)=ax^2+bx+c\,(a\ne 0)\) é o intervalo de valores de \(y\) que a parábola assume no plano. Ela depende do sinal de \(a\) (concavidade) e do vértice \(V(x_v,y_v)\).
![Imagem da função quadrática: gráfico com parábolas abrindo para cima e para baixo, indicando intervalos [y_v,+∞) e (-∞,y_v].](https://matematicahoje.blog/wp-content/uploads/2025/09/Imagem-da-Funcao-quadratica.png)
1) Pela fórmula do vértice (usando o discriminante)
Calcule o discriminante \(\Delta=b^2-4ac\). Em seguida:
\(x_v=-\dfrac{b}{2a}\)
\(y_v=-\dfrac{\Delta}{4a}\)
Se \(a>0\): \(\operatorname{Im}(f)=[y_v,+\infty)\)
Se \(a<0\): \(\operatorname{Im}(f)=(-\infty,y_v]\)
2) Pela forma canônica (completar quadrados)
Reescreva \(f(x)\) como \(f(x)=a(x-h)^2+k\). O vértice é \(V=(h,k)\), então:
Se \(a>0\): \(\operatorname{Im}(f)=[k,+\infty)\)
Se \(a<0\): \(\operatorname{Im}(f)=(-\infty,k]\)
Precisa das fórmulas sempre à mão? Baixe o eBook de Fórmulas de Matemática com as identidades e relações mais usadas em funções quadráticas e muito mais. Ideal para revisão rápida e vestibulares.
Exemplos resolvidos (contas em coluna)
Exemplo 1 — \(f(x)=x^2-4x+5\)
Objetivo: achar \(\Delta\), \(V(x_v,y_v)\) e a imagem.
Delta
\(\Delta=b^2-4ac\)
\(=(-4)^2-4\cdot 1\cdot 5\)
\(=16-20\)
\(=-4\)
Vértice
\(x_v=-\dfrac{b}{2a}=-\dfrac{-4}{2\cdot 1}=2\)
\(y_v=-\dfrac{\Delta}{4a}=-\dfrac{-4}{4\cdot 1}=1\)
Imagem
Como \(a=1>0\) (parábola para cima): \(\operatorname{Im}(f)=[1,+\infty)\).
Exemplo 2 — \(g(x)=-2x^2+8x-7\)
Objetivo: achar \(\Delta\), \(V(x_v,y_v)\) e a imagem.
Delta
\(\Delta=b^2-4ac\)
\(=8^2-4\cdot(-2)\cdot(-7)\)
\(=64-56\)
\(=8\)
Vértice
\(x_v=-\dfrac{b}{2a}=-\dfrac{8}{2\cdot(-2)}=2\)
\(y_v=-\dfrac{\Delta}{4a}=-\dfrac{8}{4\cdot(-2)}=1\)
Imagem
Como \(a=-2<0\) (parábola para baixo): \(\operatorname{Im}(g)=(-\infty,1]\).
Erros comuns (e como evitar)
- Esquecer o sinal de \(a\): ele define se o intervalo “abre para cima” \([y_v,+\infty)\) ou “fecha para baixo” \((-\infty,y_v]\).
- Trocar \(x_v\) e \(y_v\): \(x_v=-\dfrac{b}{2a}\) e \(y_v=-\dfrac{\Delta}{4a}\).
- Confundir domínio com imagem: o domínio de \(ax^2+bx+c\) é \(\mathbb{R}\); quem muda é a imagem.
- Desconsiderar domínio restrito: se \(x\) está limitado (ex.: \(x\in[1,3]\)), ache o menor e o maior valor de \(f\) nesse intervalo para obter a imagem correspondente.