Inclinação da reta tangente

Inclinação da Reta Tangente — Conceito, Fórmulas e Exemplos

Inclinação da Reta Tangente

Aprenda como calcular a inclinação da reta tangente a uma curva no ponto desejado, entenda sua relação com derivadas e veja exemplos resolvidos passo a passo.

1) O que é a inclinação da reta tangente?

A inclinação da reta tangente representa a taxa de variação instantânea de uma função \(f(x)\) em um ponto específico. Geometricamente, ela indica o quão inclinada está a reta que toca a curva exatamente em um ponto \(A(a, f(a))\).

Para determinar essa inclinação, usamos a fórmula do limite:

\( m = \lim\limits_{x \to a} \dfrac{f(x) – f(a)}{x – a} \)

Essa expressão define o coeficiente angular da reta tangente desde que o limite exista.

2) Relação com a reta secante

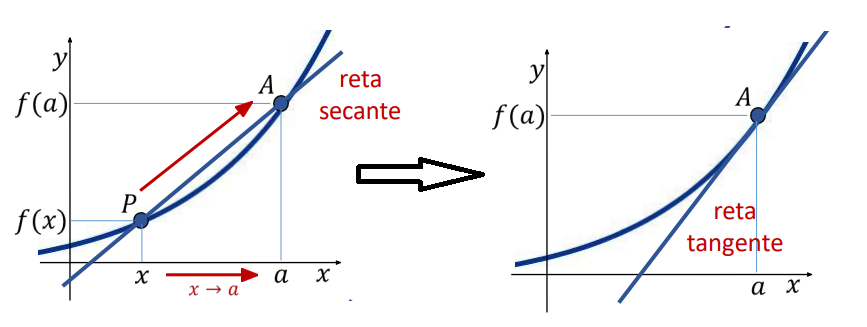
Se considerarmos dois pontos próximos \(A(a, f(a))\) e \(P(x, f(x))\) na curva, a inclinação da reta secante é:

\( m_{PA} = \dfrac{f(x) – f(a)}{x – a} \)

Quando fazemos \(x \to a\), ou seja, aproximamos os dois pontos, a reta secante se transforma na reta tangente:

\( m = \lim\limits_{x \to a} m_{PA} = \lim\limits_{x \to a} \dfrac{f(x) – f(a)}{x – a} \)

Reta tangente à curva — Visualização da reta tangente e aproximação pela reta secante.

3) Substituição por incremento \(h\)

Fazendo a substituição \(h = x – a\), temos \(x = a + h\) e, quando \(x \to a\), obtemos \(h \to 0\). A fórmula da inclinação fica:

\( m = \lim\limits_{h \to 0} \dfrac{f(a+h) – f(a)}{h} \)

Essa forma é mais prática para calcular derivadas e aparece frequentemente em exercícios.

4) Exemplo resolvido

Exemplo — Tangente à curva \(f(x) = x^2 + 1\) no ponto \(A(1,2)\)

Passo 1: Fórmula com \(h\):

\(m = \lim\limits_{h \to 0} \dfrac{f(1+h) – f(1)}{h}\)

Passo 2: Substituindo \(f(x)=x^2+1\):

\(m = \lim\limits_{h \to 0} \dfrac{(1+h)^2 + 1 – 2}{h} = \lim\limits_{h \to 0} \dfrac{h^2 + 2h}{h}\)

Passo 3: Simplificando:

\(m = \lim\limits_{h \to 0} (h + 2) = 2\)

Passo 4: Equação da reta tangente:

\(y – 2 = 2(x – 1) \Rightarrow \boxed{y = 2x}\)

Gráfico da função \(f(x)=x^2+1\) e da reta tangente \(y=2x\).

5) Leia também

Reta Tangente e Secante — relação entre derivada, taxa de variação e secantes.
Equação da Reta — conceito, formas e aplicações práticas.

Inclinação da Reta Tangente — 5 Questões por Limite (com alternativas)

Inclinação da Reta Tangente — 5 Questões por Limite

Todas as inclinações são calculadas pela definição: \[ m=\lim_{h\to0}\frac{f(a+h)-f(a)}{h} \] As alternativas ficam no enunciado; o abre/fecha aparece apenas na solução.

1) Polinomial cúbica (em \(x=2\))

Para \(f(x)=x^{3}-2x+1\), calcule a inclinação da tangente em \(x=2\) e escolha a equação correta da reta tangente.

\(y=10x-15\)
\(y=10x-5\)
\(y=5x-15\)
\(y=12x-19\)
\(y=10x+15\)

Mostrar solução (por limite)

Usamos \(m=\displaystyle\lim_{h\to0}\dfrac{f(2+h)-f(2)}{h}\).

\(f(2+h)=(2+h)^3-2(2+h)+1=8+12h+6h^2+h^3-4-2h+1\).

\(f(2)=8-4+1=5\).

Numerador: \([8+12h+6h^2+h^3-4-2h+1]-5\) \(=10h+6h^2+h^3\).

\(\dfrac{10h+6h^2+h^3}{h}=10+6h+h^2\) \(\xrightarrow[h\to0]{}10\).

Ponto: \(y_0=f(2)=5\).

Tangente: \(y-5=10(x-2)\) \(\Rightarrow y=10x-15\).

Alternativa correta: A. Inclinação \(m=10\).

2) Radical via definição (em \(x=1\))

Para \(f(x)=\sqrt{x+3}\), determine a inclinação da tangente em \(x=1\) pela definição e escolha a equação correta.

\(y=\tfrac14 x+1\)
\(y=\tfrac14 x+\tfrac{7}{4}\)
\(y=\tfrac12 x+1\)
\(y=\tfrac13 x+2\)
\(y=\tfrac14 x+2\)

Mostrar solução (por limite)

\(m=\displaystyle\lim_{h\to0}\dfrac{\sqrt{4+h}-2}{h}\).

Racionalizando: \(\dfrac{\sqrt{4+h}-2}{h}\cdot\dfrac{\sqrt{4+h}+2}{\sqrt{4+h}+2}\) \(=\dfrac{(4+h)-4}{h(\sqrt{4+h}+2)}\) \(=\dfrac{1}{\sqrt{4+h}+2}\).

Logo, \(m=\dfrac{1}{4}\).

Ponto: \(y_0=f(1)=2\).

Tangente: \(y-2=\tfrac14(x-1)\) \(\Rightarrow y=\tfrac14 x+\tfrac74\).

Alternativa correta: B. Inclinação \(m=\tfrac14\).

3) Tangente horizontal (em \(x=0\))

Para \(f(x)=\ln(x^2+1)\), determine onde a tangente é horizontal e escolha a reta correta.

\(y=0\)
\(y=1\)
\(y=x\)
\(y=-x\)
\(y=2x\)

Mostrar solução (por limite)

\(m=\displaystyle\lim_{h\to0}\dfrac{\ln((0+h)^2+1)-\ln(1)}{h}\) \(=\lim_{h\to0}\dfrac{\ln(1+h^2)}{h}\).

Substituindo \(u=h^2\): \(\dfrac{\ln(1+h^2)}{h}=\dfrac{\ln(1+u)}{u}\cdot h\).

Como \(\lim\limits_{u\to0}\dfrac{\ln(1+u)}{u}=1\), temos \(m=1\cdot 0=0\).

Ponto: \(f(0)=0\).

Tangente: \(y=0\).

Alternativa correta: A. Inclinação \(m=0\).

4) Racional por definição (em \(x=2\))

Para \(f(x)=\dfrac{x}{x-1}\), calcule \(m\) em \(x=2\) pela definição e escolha a equação correta da tangente.

\(y=-x+4\)
\(y=x-4\)
\(y=-x-2\)
\(y=x+2\)
\(y=-2x+4\)

Mostrar solução (por limite)

\(m=\displaystyle\lim_{h\to0}\dfrac{\dfrac{2+h}{1+h}-2}{h}\).

Mesmo denominador: \(\dfrac{2+h-2(1+h)}{h(1+h)}=\dfrac{-h}{h(1+h)}\).

Simplificando: \(m=-\dfrac{1}{1+h}\xrightarrow[h\to0]{}-1\).

Ponto: \(y_0=f(2)=2\).

Tangente: \(y-2=-1(x-2)\) \(\Rightarrow y=-x+4\).

Alternativa correta: A. Inclinação \(m=-1\).

5) Curva implícita (circunferência superior)

Considere \(y=\sqrt{25-x^2}\) (meia circunferência superior). Calcule a inclinação da tangente no ponto \((3,4)\) pela definição e escolha a equação correta.

\(y=-\tfrac34x+\tfrac{25}{4}\)
\(y=\tfrac34x+\tfrac{25}{4}\)
\(y=-\tfrac54x+\tfrac72\)
\(y=-\tfrac34x+4\)
\(y=\tfrac34x+4\)

Mostrar solução (por limite)

\(m=\displaystyle\lim_{h\to0}\dfrac{\sqrt{25-(3+h)^2}-4}{h}\) \(=\lim_{h\to0}\dfrac{\sqrt{16-6h-h^2}-4}{h}\).

Racionalizando: \(\dfrac{\sqrt{16-6h-h^2}-4}{h}\cdot \dfrac{\sqrt{16-6h-h^2}+4}{\sqrt{16-6h-h^2}+4}\) \(=\dfrac{-6h-h^2}{h(\sqrt{16-6h-h^2}+4)}\).

Simplificando: \(m=\dfrac{-6-h}{\sqrt{16-6h-h^2}+4}\).

Tomando o limite: \(m=\dfrac{-6}{8}=-\dfrac34\).

Tangente: \(y-4=-\tfrac34(x-3)\) \(\Rightarrow y=-\tfrac34x+\tfrac{25}{4}\).

Alternativa correta: A. Inclinação \(m=-\tfrac34\).

📚 Estudos complementares

Relacionadas

Reta Tangente e Secante

Equação da Reta

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.