Conteúdo: Estatística – Interpretação de histogramas, cálculo de média, mediana, porcentagem e frequência absoluta
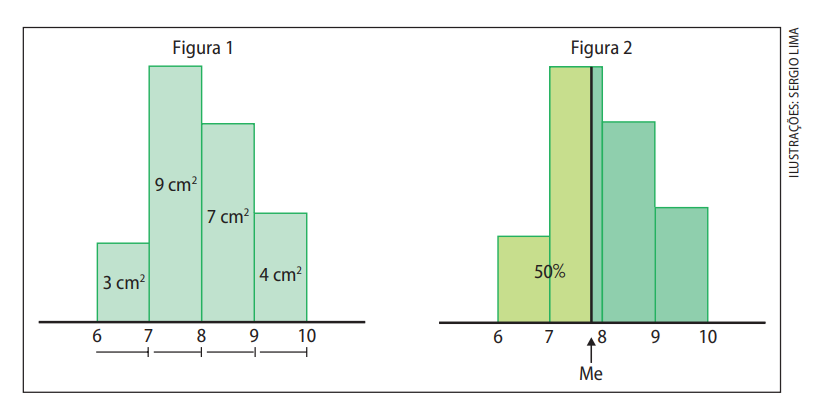
Questão 8. (Unifesp-SP) Uma prova de estatística, valendo de 0 a 10 pontos, foi realizada por 253 alunos, sendo que nenhum tirou nota menor ou igual a 6. O histograma da figura 1 indica a distribuição das notas. Ainda que o eixo com a frequência de alunos em cada faixa de notas tenha sido omitido, foi fornecida a área de cada barra do histograma. A figura 2 ilustra o cálculo da mediana das notas.
a) Calcule a porcentagem aproximada de alunos que tiraram nota menor ou igual a 7. Calcule a quantidade de alunos que tiraram nota maior que 8.
b) Calcule a média (M) e a mediana (Me) das notas usando aproximação de duas casas decimais, quando necessário.
Ver Solução
Entendendo o enunciado:
As áreas das barras representam proporcionalmente as quantidades de alunos por faixa. Vamos considerar que a soma total das áreas representa os 253 alunos.
Áreas das barras:
- 6–7: 3 cm²
- 7–8: 9 cm²
- 8–9: 7 cm²
- 9–10: 4 cm²
Total da área: \(3 + 9 + 7 + 4 = 23\)
Razão de conversão:
Cada cm² representa: \( \frac{253}{23} \approx 11\) alunos
a) Alunos com nota ≤ 7:
Faixa de 6–7: 3 cm² → \(3 × 11 = 33\) alunos
Porcentagem: \(\frac{33}{253} × 100 \approx 13\%\)
Alunos com nota > 8:
Faixas 9–10: 4 cm² → \(4 × 11 = 44\) alunos
\(\Rightarrow\) 121 alunos (soma de 7 cm² + 4 cm² = 11 cm² = \(11 × 11\))
b) Média (M) e Mediana (Me):
– Como estamos lidando com faixas, podemos usar os pontos centrais para estimar a média:
- 6,5 × 33 = 214,5
- 7,5 × 99 = 742,5
- 8,5 × 77 = 654,5
- 9,5 × 44 = 418
\[ \frac{214{,}5 + 742{,}5 + 654{,}5 + 418}{253} \approx \frac{2029{,}5}{253} \approx 8{,}02 \]
Mediana:
– O gráfico da Figura 2 mostra claramente que a mediana está na faixa 7–8, aproximadamente em 7,94.
Conclusão:
- Porcentagem com nota ≤ 7: 13%
- Alunos com nota > 8: 121 alunos
- Média \(M ≈ \mathbf{8{,}02}\)
- Mediana \(Me ≈ \mathbf{7{,}94}\)