Introdução às Integrais: Antiderivada, Primitiva e Integrais Imediatas
As integrais são um dos pilares do Cálculo. Antes da integral definida, entendemos a antiderivada (ou primitiva): dada uma função \(f(x)\), toda \(F(x)\) cuja derivada é \(F'(x)=f(x)\) é uma antiderivada de \(f\).
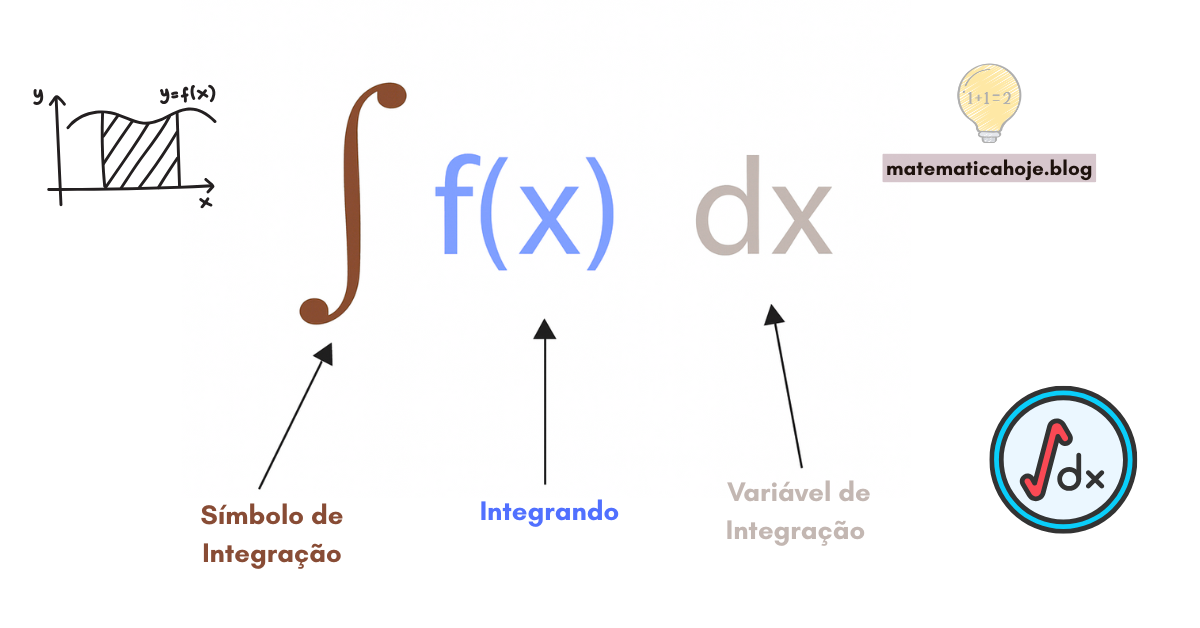
Integrais imediatas (tabela básica)
Exemplos resolvidos
1) Potência
Calcule \(\int x^3\,dx\)
👀 Ver solução
\[ \int x^3\,dx=\frac{x^{4}}{4}+C \]
2) Exponencial
Calcule \(\int e^x\,dx\)
👀 Ver solução
\[ \int e^x\,dx=e^x+C \]
3) Trigonométrica
Calcule \(\int \cos x\,dx\)
👀 Ver solução
\[ \int \cos x\,dx=\sin x+C \]
👉 Baixe o eBook Fórmulas Matemáticas
Regras essenciais (antes de praticar)
Lista de exercícios
Resolva as integrais imediatas abaixo. Observe os domínios quando surgirem logaritmos.
- \(\displaystyle \int x^5\,dx\)
- \(\displaystyle \int \frac{1}{x}\,dx\)
- \(\displaystyle \int \sin x\,dx\)
- \(\displaystyle \int 2x\,dx\)
- \(\displaystyle \int e^{2x}\,dx\)
- \(\displaystyle \int \sec^2 x\,dx\)
- \(\displaystyle \int x^{-3}\,dx\)
- \(\displaystyle \int (3x^2+2x)\,dx\)
- \(\displaystyle \int \frac{1}{1+x^2}\,dx\)
- \(\displaystyle \int \tan x\,dx\)
📘 Mostrar gabarito
- \(\displaystyle \frac{x^6}{6}+C\)
- \(\displaystyle \ln|x|+C\) (domínio: \(x\neq 0\))
- \(\displaystyle -\cos x+C\)
- \(\displaystyle x^2+C\)
- \(\displaystyle \frac{e^{2x}}{2}+C\)
- \(\displaystyle \tan x+C\)
- \(\displaystyle -\frac{1}{2x^2}+C\)
- \(\displaystyle x^3+x^2+C\)
- \(\displaystyle \arctan x+C\)
- \(\displaystyle -\ln|\cos x|+C\) (ou \(\ln|\sec x|+C\); \(\cos x\neq 0\))
Cheque por derivação
Uma forma de validar antiderivadas é derivar o resultado para ver se retornamos ao integrando.
🔎 Verificações rápidas
\[ \frac{d}{dx}\!\left(\frac{e^{2x}}{2}\right)=e^{2x}\quad\text{e}\quad \frac{d}{dx}\!\left(-\ln|\cos x|\right)=\tan x. \] \[ \frac{d}{dx}\!\left(\frac{x^{n+1}}{n+1}\right)=x^n\quad(n\neq -1). \]
👉 Método da Substituição nas Integrais
👉 Integral Definida e Áreas
👉 Mapas Mentais de Matemática













