Comportamento de Variáveis
Você já parou para pensar como o tempo e a distância se relacionam durante uma corrida? Este artigo analisa uma situação real vivida por atletas: o monitoramento da distância percorrida ao longo do tempo, especialmente nos primeiros segundos de uma arrancada. A proposta é entender o comportamento dessas variáveis e como elas se relacionam matematicamente.
A Situação: Corrida com Aceleração Constante
Um treinador está avaliando o desempenho de um atleta que está treinando para uma prova de 100 metros rasos. Ele registra o tempo e a distância percorrida nos cinco primeiros segundos da corrida, momento em que o atleta parte com aceleração constante.
Tabela de Observações
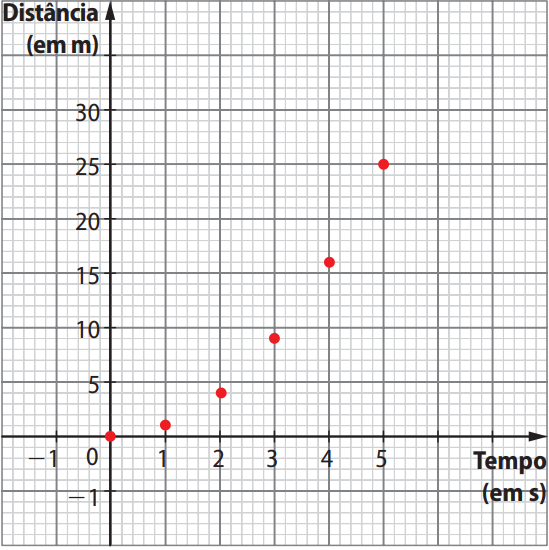
| Tempo (em segundos) | Distância (em metros) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
Análise Gráfica
Ao representar os dados em um plano cartesiano, nota-se que os pontos formam uma curva e não uma linha reta. Isso indica que as variáveis tempo e distância não são diretamente proporcionais.
Na proporção direta, espera-se que dobrando o tempo, dobre-se a distância. Mas aqui, o que se observa é que:
- Para t = 2 s, a distância é 4 m (2²)
- Para t = 3 s, a distância é 9 m (3²)
- Para t = 4 s, a distância é 16 m (4²)
- Para t = 5 s, a distância é 25 m (5²)
Logo, a relação é do tipo quadrática:
d = t²
Interpretação Matemática
A equação acima nos mostra que o tempo é a variável independente e que a distância aumenta ao quadrado do tempo. Esse padrão é típico de movimentos com aceleração constante a partir do repouso.
Na física, esse comportamento é representado pela fórmula:
S = S₀ + v₀t + (1/2)at²
No caso do nosso exemplo:
- S₀ = 0 (partida da origem)
- v₀ = 0 (início com velocidade nula)
- Logo, S = (1/2)at²
Portanto, a equação d = t² sugere uma aceleração de 2 m/s², já que (1/2)a = 1.
Conclusão: A Matemática no Esporte
Este exemplo simples mostra como a matemática está presente no cotidiano de um atleta. Compreender a relação entre tempo e distância ajuda a traçar estratégias de treino mais eficientes e a monitorar a evolução do desempenho.
Além disso, o estudo gráfico e numérico dessas variáveis desenvolve o pensamento analítico, tão valorizado dentro e fora da sala de aula.
A busca por tempos menores é parte essencial da evolução de um atleta de corrida — e a matemática pode ser uma grande aliada nessa jornada!
🧠 Baixe Mapas Mentais de Matemática