ITA 2023 — 1ª Fase — Questão 44 — Geometria Analítica
Considere a hipérbole \( H \) de equação \( \frac{x^2}{1} – \frac{y^2}{4} = 1 \).
Seja \( T \) um triângulo de vértices \( P, F_1, F_2 \), onde \( F_1 \) e \( F_2 \) são os focos de \( H \) e \( F \) um ponto em \( H \).
Sabendo que o perímetro de \( T \) é \( 5\sqrt{5} \), o produto da medida dos lados de \( T \) é:
a) \( \frac{41\sqrt{5}}{2} \) b) \( \frac{41}{4} \) c) \( \frac{41\sqrt{5}}{4} \) d) \( \frac{41}{8} \) e) \( \frac{41\sqrt{5}}{8} \)
a) \( \frac{41\sqrt{5}}{2} \) b) \( \frac{41}{4} \) c) \( \frac{41\sqrt{5}}{4} \) d) \( \frac{41}{8} \) e) \( \frac{41\sqrt{5}}{8} \)
👀 Solução passo a passo
1) Dados da hipérbole:
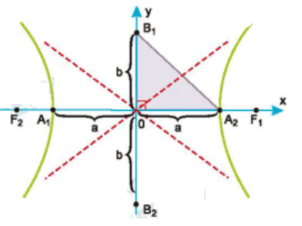A equação:
\[
\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1
\]
fornece \( a^2 = 1 \), \( b^2 = 4 \), logo \( a = 1 \) e \( b = 2 \).
A distância focal:
\[
f = \sqrt{a^2 + b^2} = \sqrt{1 + 4} = \sqrt{5}.
\]
Assim, os focos são:
\[
F_1(\sqrt{5}, 0), \quad F_2(-\sqrt{5}, 0)
\]
e a distância \( F_1F_2 = 2\sqrt{5} \).2) Condições para \(P\) na hipérbole:
Pela definição, \(|PF_1 – PF_2| = 2a = 2\). Adotando \(PF_1 > PF_2\): \[ \begin{cases} PF_1 – PF_2 = 2 \\ PF_1 + PF_2 + F_1F_2 = 5\sqrt{5} \end{cases} \] Substituindo \(F_1F_2 = 2\sqrt{5}\): \[ PF_1 + PF_2 + 2\sqrt{5} = 5\sqrt{5} \Rightarrow PF_1 + PF_2 = 3\sqrt{5}. \]3) Resolvendo o sistema:
\[ \begin{cases} PF_1 – PF_2 = 2 \\ PF_1 + PF_2 = 3\sqrt{5} \end{cases} \] Somando e subtraindo: \[ PF_1 = \frac{3\sqrt{5} + 2}{2}, \quad PF_2 = \frac{3\sqrt{5} – 2}{2}. \]4) Produto das medidas dos lados:
O triângulo tem lados \(PF_1\), \(PF_2\) e \(F_1F_2 = 2\sqrt{5}\). Assim: \[ \left( \frac{3\sqrt{5} + 2}{2} \right) \cdot \left( \frac{3\sqrt{5} – 2}{2} \right) \cdot 2\sqrt{5} \] \[ = \frac{(3\sqrt{5})^2 – 2^2}{4} \cdot 2\sqrt{5} = \frac{45 – 4}{4} \cdot 2\sqrt{5} = \frac{41}{4} \cdot 2\sqrt{5} = \frac{41\sqrt{5}}{2}. \]
Pela definição, \(|PF_1 – PF_2| = 2a = 2\). Adotando \(PF_1 > PF_2\): \[ \begin{cases} PF_1 – PF_2 = 2 \\ PF_1 + PF_2 + F_1F_2 = 5\sqrt{5} \end{cases} \] Substituindo \(F_1F_2 = 2\sqrt{5}\): \[ PF_1 + PF_2 + 2\sqrt{5} = 5\sqrt{5} \Rightarrow PF_1 + PF_2 = 3\sqrt{5}. \]3) Resolvendo o sistema:
\[ \begin{cases} PF_1 – PF_2 = 2 \\ PF_1 + PF_2 = 3\sqrt{5} \end{cases} \] Somando e subtraindo: \[ PF_1 = \frac{3\sqrt{5} + 2}{2}, \quad PF_2 = \frac{3\sqrt{5} – 2}{2}. \]4) Produto das medidas dos lados:
O triângulo tem lados \(PF_1\), \(PF_2\) e \(F_1F_2 = 2\sqrt{5}\). Assim: \[ \left( \frac{3\sqrt{5} + 2}{2} \right) \cdot \left( \frac{3\sqrt{5} – 2}{2} \right) \cdot 2\sqrt{5} \] \[ = \frac{(3\sqrt{5})^2 – 2^2}{4} \cdot 2\sqrt{5} = \frac{45 – 4}{4} \cdot 2\sqrt{5} = \frac{41}{4} \cdot 2\sqrt{5} = \frac{41\sqrt{5}}{2}. \]
Resposta: \( \frac{41\sqrt{5}}{2} \) — Alternativa **A**
