Questão 06 — ITA 2025 — 1ª Fase | Conteúdo: Equações exponenciais • Análise de raízes
O conjunto de todos os valores \(a \in \mathbb{R}\) para os quais a equação
\[ 9^{x} – (3a+4)\,3^{x} + 2a^{2} + 9a – 5 = 0 \]tem duas soluções reais distintas é:
👀 Solução passo a passo
1) Substituição \(t=3^x>0\)
Como \(9^x=(3^x)^2\), a equação vira um quadrático em \(t\):
\[ t^2 – (3a+4)t + (2a^2+9a-5)=0,\quad t=3^x>0. \]Para obter **duas soluções reais distintas em \(x\)**, o quadrático deve ter **duas raízes reais positivas**.
2) Discriminante estritamente positivo
\[
\Delta=(3a+4)^2-4(2a^2+9a-5)
=a^2-12a+36=(a-6)^2.
\]
Exigir duas raízes reais distintas \(\Rightarrow \Delta>0 \Rightarrow a\ne 6.\)
3) Raízes positivas (soma e produto)
Sejam \(r_1,r_2\) as raízes do quadrático. Para \(r_1,r_2>0\):
\[ \underbrace{r_1+r_2}_{=\,3a+4} > 0 \ \Rightarrow\ a>-\tfrac{4}{3}, \] \[ \underbrace{r_1r_2}_{=\,2a^2+9a-5} > 0. \]Fatorando \(2a^2+9a-5=2(a+5)\left(a-\tfrac12\right)\) (raízes \(-5\) e \(\tfrac12\)), temos:
\[ r_1r_2>0 \ \Leftrightarrow\ a< -5 \ \text{ ou }\ a> \tfrac12. \]Com a condição da soma \((a>-\tfrac{4}{3})\), sobra \(a>\tfrac12\).
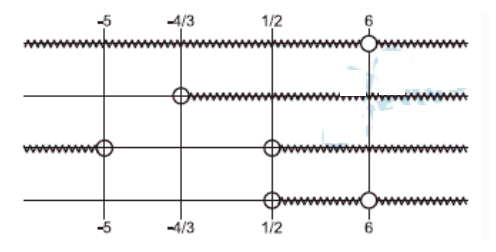
4) Conclusão
Conjunto solução para \(a\):
\[
\left(\tfrac{1}{2},\ \infty\right)\setminus\{6\}.
\]
Gabarito: b).






















