Considere a função
\[ f(x)=\sqrt{\frac{2\sin(2x)+2\sin(x)-2\cos(x)-1}{8\left(\cos(2x)+1\right)}}. \]Seja \(I=(a,b)\) o intervalo de maior comprimento contido em \([-\pi,2\pi]\) tal que \(f(x)\) está definida para todo \(x\in I\). O valor de \(a+b\) é:
👀 Solução passo a passo
Usando \(\sin(2x)=2\sin x\cos x\) e \(\cos(2x)=2\cos^2 x-1\):
\[ f(x)=\sqrt{\frac{4\sin x\cos x+2\sin x-2\cos x-1}{8(2\cos^2 x)}} =\sqrt{\frac{(2\sin x-1)(2\cos x+1)}{16\cos^2 x}}. \]Como há raiz, precisamos do radicando \(\ge 0\) e \(\cos x\ne 0\).
O produto \(\ge 0\) ocorre em dois casos:
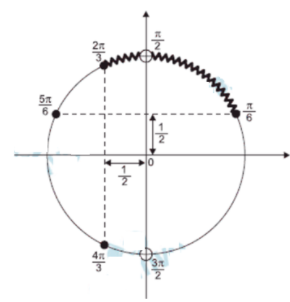
I) \(\sin x \ge \tfrac{1}{2}\) e \(\cos x \ge -\tfrac{1}{2}\) (com \(\cos x\ne 0\)).
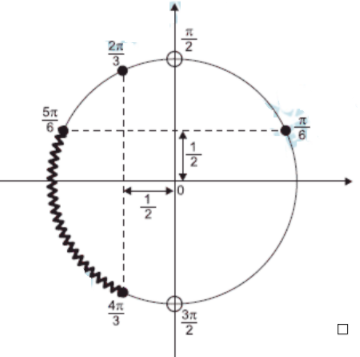
II) \(\sin x \le \tfrac{1}{2}\) e \(\cos x \le -\tfrac{1}{2}\) (com \(\cos x\ne 0\)).
• Caso I: \(x\in \big[\tfrac{\pi}{6},\tfrac{\pi}{2}\big)\ \cup\ \big(\tfrac{\pi}{2},\tfrac{2\pi}{3}\big]\).
• Caso II: \(x\in \big[-\pi,-\tfrac{2\pi}{3}\big]\ \cup\ \big[\tfrac{5\pi}{6},\tfrac{4\pi}{3}\big]\).
(Exclui-se \(\cos x=0\): \(x=\tfrac{\pi}{2},\tfrac{3\pi}{2}\).)
é o maior intervalo contido em \([-\pi,2\pi]\) onde \(f(x)\) está definida.






















