Seja \(ABC\) um triângulo de lados \(m(\overline{AB})=6\), \(m(\overline{AC})=10\) e \(m(\overline{BC})=14\). Calcule o raio \(r\) da circunferência externa ao triângulo \(ABC\) que tangencia simultaneamente o segmento \(\overline{BC}\) e as retas suportes \(AB\) e \(AC\).
👀 Solução passo a passo
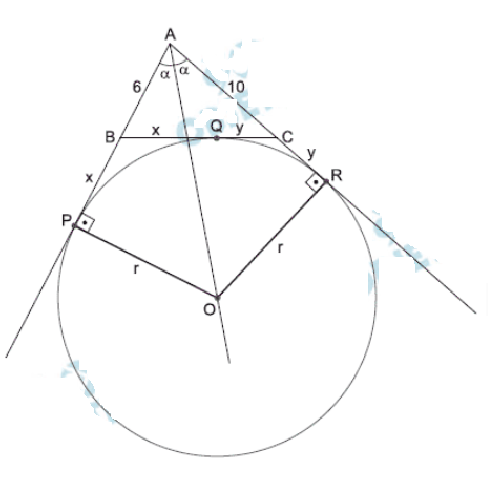
Sejam \(P\) e \(R\) os pontos de tangência da circunferência com as retas suportes \(AB\) e \(AC\), respectivamente, e \(Q\) o ponto de tangência com o segmento \(\overline{BC}\). Denote \(BQ=x\) e \(QC=y\). Como \(BC=14\),
\[ x+y=14. \tag{I} \]Pelas tangências a partir do mesmo ponto \(A\), os segmentos de tangência são iguais: \(AP=AR\). Observando que \(AP = AB + BQ = 6 + x\) e \(AR = AC + CQ = 10 + y\), obtemos
\[ 6 + x = 10 + y \ \Rightarrow\ x – y = 4. \tag{II} \]De (I) e (II): \(x=9\) e \(y=5\).
No triângulo \(ABC\), com lados \(AB=6\), \(AC=10\), \(BC=14\):
\[ 14^2 = 6^2 + 10^2 – 2\cdot 6\cdot 10 \cos(2\alpha) \ \Rightarrow\ \cos(2\alpha) = -\frac{1}{2}. \]Logo, \(2\alpha=120^\circ \Rightarrow \alpha=60^\circ\).
Se \(O\) é o centro da circunferência, então o raio \(r\) é perpendicular às tangentes em \(P,Q,R\). No triângulo \(APO\), o ângulo em \(A\) é \(\alpha=60^\circ\) e \(AP=6+x=15\). Pela definição de tangente no triângulo retângulo \(APO\):
\[ \tan\alpha=\frac{PO}{AP}=\frac{r}{15}. \]Como \(\tan60^\circ=\sqrt{3}\), segue:
\[ \sqrt{3}=\frac{r}{15}\ \Rightarrow\ r=15\sqrt{3}. \]





















