Juros Compostos: Fórmulas, Exemplos e Exercícios Resolvidos
Aprenda a calcular valor futuro, valor presente e taxa em juros compostos, com passos linha a linha para tela pequena.
O que são Juros Compostos?
Nos juros compostos, os juros de cada período são incorporados ao capital, gerando novos juros (“juros sobre juros”). Por isso o crescimento é exponencial, sendo o padrão de investimentos, financiamentos e parcelamentos.
Fórmulas fundamentais
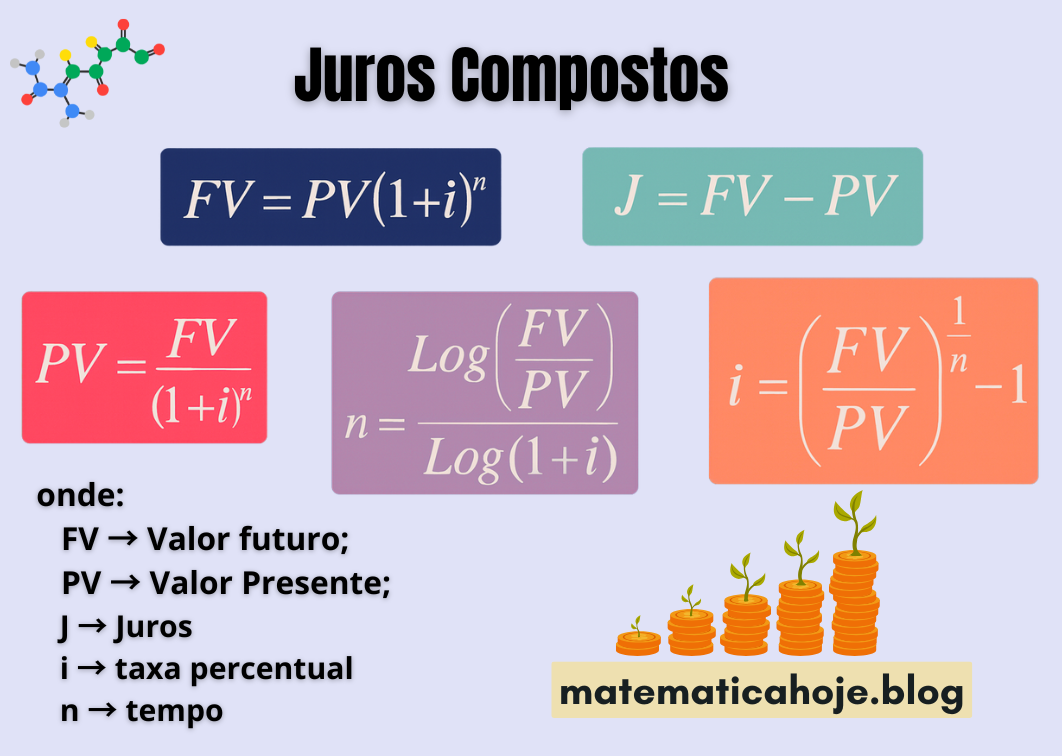
Valor Futuro (Montante)
\( FV = PV(1+i)^n \)
Valor Presente
\( PV = \dfrac{FV}{(1+i)^n} \)
Taxa
\( i = \left(\dfrac{FV}{PV}\right)^{\tfrac{1}{n}} – 1 \)
Onde: \(FV\) valor futuro; \(PV\) valor presente; \(i\) taxa por período (decimal); \(n\) número de períodos; \(J = FV – PV\) são os juros.
📘 Materiais que aceleram seus resultados
Baixe o eBook Fórmulas Matemática (gratuito) e revise visualmente com os Mapas Mentais de Matemática. Para treinar mais: Banco de Questões e 10 eBooks de Matemática. Conteúdos para o ENEM Matemática.
Exemplos resolvidos (passo a passo)
Exemplo 1 — Montante
Enunciado: R$ 2.000,00 a 5% a.m. por 6 meses. Calcule o valor futuro.
Solução:
\( FV = PV(1+i)^n \)
\( FV = 2000(1+0{,}05)^6 \)
\( FV = 2000 \times 1{,}3401 \)
\( FV = \mathbf{R\$\,2680{,}20} \)
Exemplo 2 — Valor presente
Enunciado: Quanto devo aplicar hoje para ter R$ 5.000,00 em 8 meses, a 3% a.m.?
Solução:
\( PV = \dfrac{FV}{(1+i)^n} \)
\( PV = \dfrac{5000}{(1+0{,}03)^8} \)
\( PV = \dfrac{5000}{1{,}2668} \)
\( PV = \mathbf{R\$\,3946{,}78} \)
Exercícios de Juros Compostos
Tente resolver e depois abra para conferir. Nas contas, colocamos uma etapa por linha para ficar legível no celular.
1) (Múltipla escolha) R$ 1.000,00 a 10% a.m. por 4 meses. O montante é:
- A) R$ 1.410,00
- B) R$ 1.464,10
- C) R$ 1.500,00
- D) R$ 1.464,00
Ver solução
\( FV = 1000 \times 1{,}4641 \)
\( FV = \mathbf{R\$\,1.464{,}10} \)
Alternativa: B.
2) (Discursiva) Qual o PV para obter R$ 3.000,00 em 10 meses a 2% a.m.?
Ver solução
\( PV = \dfrac{3000}{1{,}21899} \)
\( PV = \mathbf{R\$\,2461{,}76} \)
3) (Múltipla escolha) R$ 5.000,00 a 4% a.m. por 3 meses. O montante é:
- A) R$ 5.520,00
- B) R$ 5.624,32
- C) R$ 5.612,00
- D) R$ 5.700,00
Ver solução
\( FV = 5000 \times 1{,}124864 \)
\( FV = \mathbf{R\$\,5.624{,}32} \)
Alternativa: B.
4) (Discursiva) Em 24 meses a 1,2% a.m., quanto vira um capital de R$ 7.500,00?
Ver solução
\( FV = 7500 \times 1{,}319 \) (aprox.)
\( FV \approx \mathbf{R\$\,9.892{,}50} \)
5) (Múltipla escolha) Um capital dobra em 36 meses. A taxa mensal composta é, aproximadamente:
- A) 2,0% a.m.
- B) 1,9% a.m.
- C) 1,7% a.m.
- D) 1,6% a.m.
Ver solução
\( i \approx 0{,}0193 = \mathbf{1{,}93\%\ a.m.} \)
Alternativa: B.
6) (Discursiva) Qual taxa mensal gera R$ 4.000,00 a partir de R$ 3.200,00 em 8 meses?
Ver solução
\( i = (4000/3200)^{1/8}-1 \)
\( i = (1{,}25)^{0{,}125}-1 \)
\( i \approx \mathbf{2{,}84\%\ a.m.} \)
7) (Múltipla escolha) Um investimento rende 0,8% a.m. Em 18 meses, o fator de capitalização é:
- A) 1,144
- B) 1,150
- C) 1,160
- D) 1,200
Ver solução
Alternativa mais próxima: B) 1,150.
8) (Discursiva) Você quer R$ 50.000,00 em 5 anos a 1% ao mês. Qual o depósito único hoje?
Ver solução
\( PV = \dfrac{50000}{1{,}8167} \)
\( PV \approx \mathbf{R\$\,27.515{,}00} \)
Mais prática? Acesse: Banco de Questões de Matemática, 10 eBooks e o guia ENEM Matemática.













