Lei dos Senos
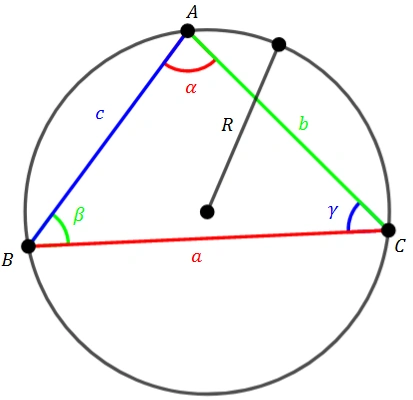
A Lei dos Senos relaciona os lados de um triângulo a seus ângulos opostos e ao circunrádio \(R\). É a ferramenta padrão para resolver triângulos qualquer quando temos pares lado ↔ ângulo.
Fórmula
Quando usar (e quando não)
AAS/ASA: dois ângulos e um lado ⇒ calcule o terceiro ângulo e, depois, os lados com a Lei dos Senos.
SSA: dois lados e um ângulo não compreendido ⇒ pode haver 0, 1 ou 2 soluções (caso ambíguo).
Com circunrádio: conhecendo \(R\), \(a=2R\sin\alpha\) (e cíclicas). Veja também área do triângulo para integrar os resultados.
Demonstrações curtas
1) Pela circunferência (cordas)
No círculo de raio \(R\), a corda oposta a \(\alpha\) tem comprimento \(a=2R\sin\alpha\). Repetindo para \(b\) e \(c\) obtemos a igualdade com \(2R\).
2) Pela área
\(A=\dfrac{1}{2}bc\sin\alpha=\dfrac{1}{2}ac\sin\beta=\dfrac{1}{2}ab\sin\gamma\). Isolando \( \dfrac{a}{\sin\alpha},\dfrac{b}{\sin\beta},\dfrac{c}{\sin\gamma}\) nota-se que são iguais; pela prova anterior, a constante é \(2R\). (Conecte com todas as fórmulas de área.)
Exemplos resolvidos (situação-problema)
Exemplo 1 — Encontrar lado (AAS)
Projeto de cerca: na maquete de um terreno triangular, \(\alpha=40^\circ\), \(\beta=75^\circ\) e o lado oposto a \(\beta\) mede \(b=12\). Qual o comprimento \(a\) da cerca oposta a \(\alpha\)?
Ver solução
Exemplo 2 — Encontrar ângulo (SSA sem ambiguidade)
Peça de metal: duas barras opostas medem \(a=10\) e \(b=14\). O ângulo na barra \(a\) é \(\alpha=30^\circ\). Qual deve ser o ângulo \(\beta\) para a junção?
Ver solução
Exemplo 3 — Caso ambíguo (SSA com 2 soluções)
Molde de tecido: bordas correspondem a \(a=9\) e \(b=12\); o ângulo em \(a\) vale \(\alpha=40^\circ\). Quais são as possíveis aberturas \(\beta\)?
Ver solução
Exemplo 4 — Usando o circunrádio
Emblema no aro: um triângulo deve ser inscrito num aro de raio \(R=5\) com \(\alpha=72^\circ\). Qual deve ser o lado oposto \(a\)?
Ver solução
Exemplo 5 — Área ligada à Lei dos Senos
Placa triangular: lados \(b=10\) e \(c=12\) formam \(\alpha=35^\circ\). Qual é a área \(A\) para a pintura?
Ver solução
Erros comuns (e como evitar)
Pares trocados. Sempre use \(a\leftrightarrow\alpha\), \(b\leftrightarrow\beta\), \(c\leftrightarrow\gamma\).
Ignorar o caso ambíguo (SSA). Verifique também \(180^\circ-\arcsin(\,)\) quando compatível. Se necessário, confirme com a Lei dos Cossenos.
Modo da calculadora. Confira se está em graus/radianos; saiba converter em trigonometria básica.
Arredondamento precoce. Guarde mais casas e arredonde no fim.
Exercícios propostos
1) \( \alpha=28^\circ\), \( \beta=61^\circ\), \( c=12 \). Calcule \(a\) e \(b\).
2) \( a=7\), \( b=11\), \( \alpha=35^\circ\). Encontre \(\beta\) (avalie o caso ambíguo).
3) \(R=6\) e \(\gamma=48^\circ\). Determine \(c\) e, sabendo \(a=9\), encontre \(\alpha\).
4) Placa triangular com \(b=15\), \(c=18\) e \(\alpha=50^\circ\). Calcule a área. (Dica: use \(A=\frac{1}{2}bc\sin\alpha\)).
Continue estudando (linkagem interna)
Lei dos Cossenos — complete a resolução de triângulos com a relação entre lados e ângulo compreendido.
Área do Triângulo — todas as fórmulas (base–altura, 2 lados + ângulo, Heron, circunrádio/inrário).
Pontos Notáveis do Triângulo — entenda o circuncentro (fornece \(R\)) e o incentro (fornece \(r\)).
Razões Trigonométricas — seno, cosseno e tangente, com visão geométrica.
Triângulos: tipos e propriedades — revisite ângulos internos, soma \(180^\circ\) e classificações.