Leitura e interpretação de gráficos
Passo a passo, armadilhas comuns e exercícios — com base em um gráfico real de evolução de bactérias.
Gráficos aparecem em provas, relatórios e no dia a dia. Para ir além de “olhar” e realmente interpretar, conecte o gráfico ao Plano Cartesiano, ao conceito de Gráfico de uma Função e à leitura de Pontos no Plano. Para treinar bastante, use o Banco de Questões.
Passo a passo universal para ler um gráfico
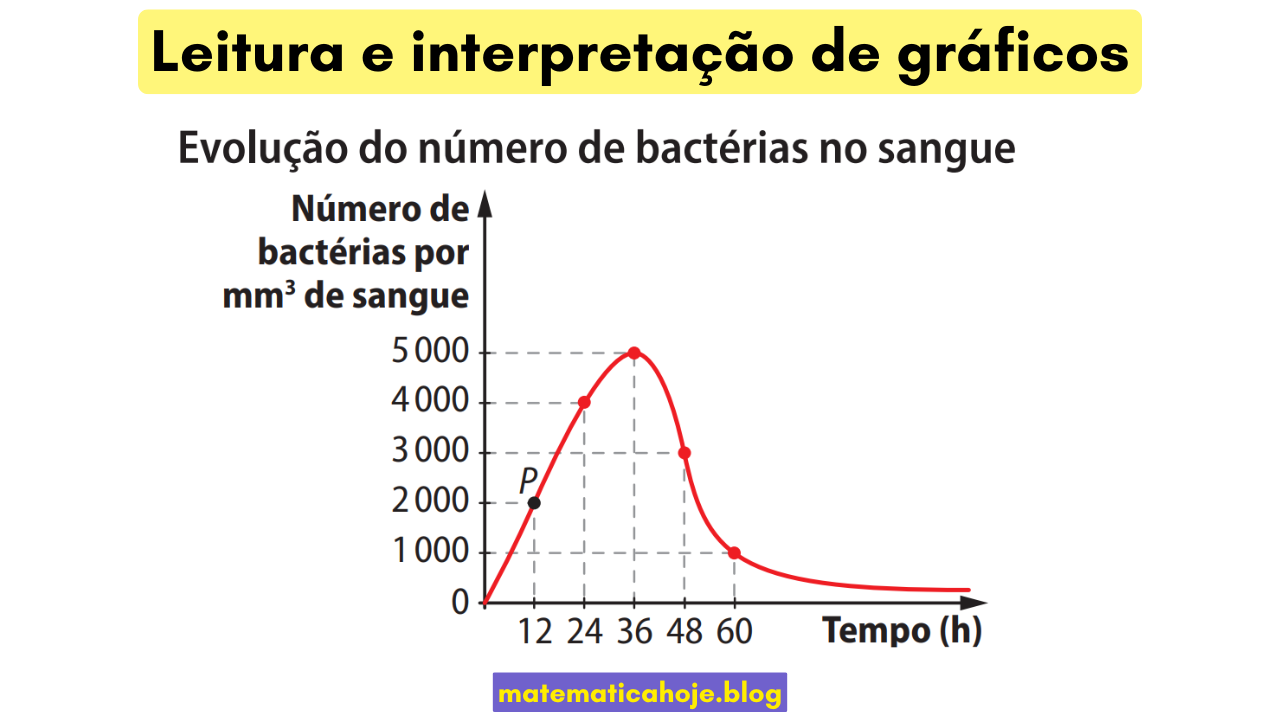
- Identifique eixos, unidades e título. Aqui: tempo (h) no eixo \(x\) e “nº de bactérias por mm³” no eixo \(y\).
- Cheque a escala (saltos iguais ou não? começa em zero?).
- Localize pontos de interesse: picos (máximos), vales (mínimos), interceptos e mudanças de tendência.
- Compare intervalos pelo “inclinar” da curva (taxa de variação = quão íngreme).
- Atenção a previsões: interpolação (entre pontos medidos) é mais segura que extrapolação (fora do intervalo observado).
O que o gráfico da figura nos conta
- De 0 a 36 h, a população cresce e atinge um máximo ≈ 5 000 bactérias/mm³ em \(36\) h.
- Há leituras destacadas: \(12\) h → ≈ 2 000; \(24\) h → ≈ 4 000; \(48\) h → ≈ 3 000; \(60\) h → ≈ 1 000.
- Depois de 60 h, a curva decai e se aproxima de valores baixos (tendência a estabilizar próximo de 0, sem ficar negativa).
Tipos comuns de gráfico e como não cair em armadilhas
| Tipo | Quando usar | Cuidados |
|---|---|---|
| Linha/Curva | Evolução temporal, tendências e taxas | Escalas não uniformes e cortes no eixo \(y\) podem exagerar variações |
| Barras | Comparar categorias | Ordenação pode induzir leitura; comece em zero para evitar distorção |
| Colunas acumuladas | Partes de um total por período | Difícil comparar componentes não alinhados |
| Pizza | Proporções de um todo | Evite muitos setores; ângulos são difíceis de comparar |
| Histograma | Distribuição de dados contínuos | Largura das classes altera a percepção |
| Dispersão | Correlação entre duas variáveis | Não confundir correlação com causalidade |
Exemplos rápidos com a figura
Leitura pontual
Em \(x=24\) h, leia na vertical até a curva e depois na horizontal: aproximadamente 4 000 bactérias/mm³.
Taxa média
De 24 h a 36 h: \(\dfrac{5000-4000}{36-24}=\dfrac{1000}{12}\approx 83\) por hora.
Intervalo de queda mais acentuada
De 36 h a 48 h a curva despenca de 5 000 para 3 000: queda média de ~167 por hora (mais íngreme que de 48→60 h).
Exercícios (múltipla escolha) com solução
1) Pelo gráfico, o valor em \(x=36\) h é aproximadamente:
- 3 000
- 4 000
- 5 000
- 6 000
Ver solução
2) O instante do pico da população bacteriana é aproximadamente:
- 24 h
- 36 h
- 48 h
- 60 h
Ver solução
3) Em qual intervalo a taxa de diminuição é mais intensa?
- 12–24 h
- 24–36 h
- 36–48 h
- 48–60 h
Ver solução
4) A taxa média de crescimento entre 0 h e 24 h é, em bactérias/mm³ por hora, aproximadamente:
- 90
- 120
- 170
- 220
Ver solução
5) Usando interpolação linear entre 24 h (4 000) e 36 h (5 000), a estimativa para 30 h é:
- 4 250
- 4 500
- 4 750
- 5 250
Ver solução
6) Sobre a tendência após 60 h, a afirmação coerente é:
- A curva torna-se negativa.
- O número continua caindo e se aproxima de zero.
- Há um novo pico maior que 5 000.
- Permanece constante em 1 000.
Ver solução
Glossário rápido
- Taxa média: \(\Delta y/\Delta x\) em um intervalo.
- Interpolação: estimar entre pontos medidos (mais seguro).
- Extrapolação: estimar fora do intervalo observado (cautela!).
- Máximo/Mínimo: maior/menor valor observado (local ou global).
Continue estudando (links internos)
• Gráfico de uma Função
• Plano Cartesiano
• Ponto no Plano Cartesiano
• Roteiro ENEM Matemática
• Coleção 10 eBooks de Matemática





















