Logaritmo: definição, propriedades e exemplos resolvidos
O logaritmo é uma das ferramentas matemáticas mais importantes, com aplicações em provas do ENEM, concursos, ciências naturais e tecnologia. Ele surge como o expoente ao qual uma base deve ser elevada para gerar um número.
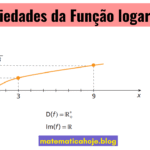
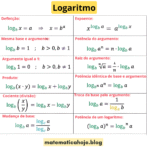
Definição de logaritmo
Exemplos básicos
- \(\log_{2} 8 = 3 \quad\) pois \(2^3=8\).
- \(\log_{5} 125 = 3 \quad\) pois \(5^3=125\).
- \(\log_{10} 0,01 = -2 \quad\) pois \(10^{-2}=0,01\).
Consequências da definição
- \(\log_{a} 1 = 0\) (qualquer base válida elevada a 0 dá 1).
- \(\log_{a} a = 1\).
- \(\log_{a} b = c \iff b=a^{c}\).
- Não existe logaritmo de número negativo nem de base negativa.
Exemplos resolvidos
Exemplo 1: Resolva \(\log_{3} 81\)
Como \(81=3^4\), então \(\log_{3} 81=4\).
Exemplo 2: Resolva \(\log_{5} \tfrac{1}{125}\)
\(\tfrac{1}{125}=5^{-3}\), logo \(\log_{5}\tfrac{1}{125}=-3\).
Exemplo 3: Resolva \(\log_{2} x = 7\)
\(\log_{2} x = 7 \iff 2^{7}=x \iff x=128\).
Logaritmos decimais e na calculadora
O logaritmo decimal (base 10) é indicado por \(\log x\). Exemplo: \(\log 1000 = 3\).
Nas calculadoras científicas, o botão log fornece logaritmos de base 10 e o botão ln fornece logaritmos de base \(e\) (número de Euler).
Exercícios práticos
- \(\log_{2} 32\)
- \(\log_{3} 81\)
- \(\log_{10} 0,001\)
- Resolva: \(\log_{5} x = 4\)
Gabarito
1) 5. 2) 4. 3) -3. 4) \(x=625\).
📥 Reforce seus estudos
Baixe nosso eBook de Fórmulas Matemáticas com todas as propriedades dos logaritmos e potenciação.
Baixar agoraConclusão
O logaritmo é o inverso da potência. Ele facilita cálculos, simplifica equações e é essencial para questões de concursos, estatística e ciências. Compreender sua definição e propriedades é fundamental para avançar em Matemática Básica e Avançada.