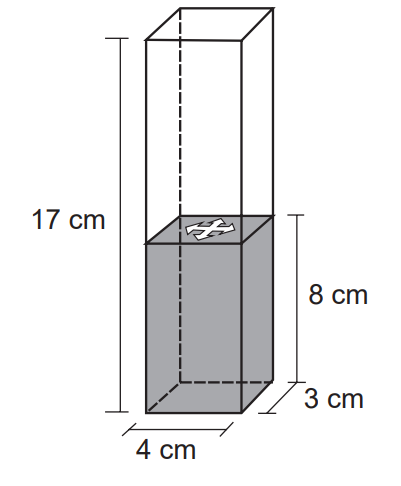
Num recipiente com a forma de paralelepípedo reto-retângulo, colocou-se água até a altura de 8 cm e um objeto, que ficou flutuando na superfície da água. Para retirar o objeto de dentro do recipiente, a altura da coluna de água deve ser de, pelo menos, 15 cm. Para a coluna de água chegar até essa altura, é necessário colocar dentro do recipiente bolinhas de volume igual a 6 cm³ cada, que ficarão totalmente submersas.
O número mínimo de bolinhas necessárias para que se possa retirar o objeto que flutua na água, seguindo as instruções dadas, é de
- 14.
- 16.
- 18.
- 30.
- 34.
Mostrar / esconder solução passo a passo
1) Volume necessário para elevar o nível
A altura deve aumentar \(15-8=7\) cm. Como a base mede \(4\ \text{cm}\times 3\ \text{cm}\), \[ \Delta V = 4\cdot 3 \cdot 7 = 84\ \text{cm}^3. \]
A altura deve aumentar \(15-8=7\) cm. Como a base mede \(4\ \text{cm}\times 3\ \text{cm}\), \[ \Delta V = 4\cdot 3 \cdot 7 = 84\ \text{cm}^3. \]
2) Volume deslocado pelas bolinhas
Cada bolinha (totalmente submersa) desloca \(6\ \text{cm}^3\). Logo, com \(n\) bolinhas: \[ 6n = 84 \;\Rightarrow\; n = 14. \]
Cada bolinha (totalmente submersa) desloca \(6\ \text{cm}^3\). Logo, com \(n\) bolinhas: \[ 6n = 84 \;\Rightarrow\; n = 14. \]
Gabarito: letra A — 14 bolinhas.
Questão anterior (ENEM 2020 Matemática)
Questão 38 — envasamento e altura do líquido
.
Banco de Questões do ENEM (Matemática)
acessar agora.
Mapas Mentais de Matemática
ver mapas.
10 eBooks de Matemática
baixar eBooks.























