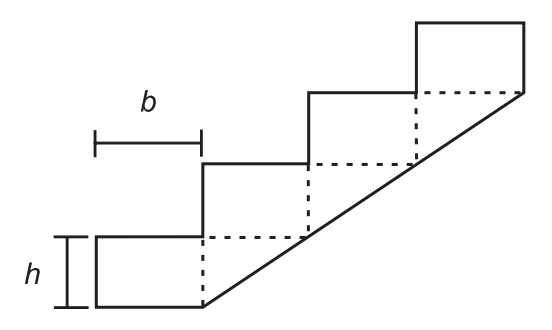
Uma casa de dois andares está sendo projetada. É necessário incluir no projeto a construção de uma escada para o acesso ao segundo andar. Para o cálculo das dimensões dos degraus utilizam-se as regras: \( \lvert 2h + b – 63{,}5 \rvert \le 1{,}5 \) e \( 16 \le h \le 19 \), nas quais \(h\) é a altura do degrau (denominada espelho) e \(b\) é a profundidade da pisada, como mostra a figura. Por conveniência, escolheu-se a altura do degrau como sendo \( h = 16 \). As unidades de \(h\) e \(b\) estão em centímetro.
Nesse caso, o mais amplo intervalo numérico ao qual a profundidade da pisada (\(b\)) deve pertencer, para que as regras sejam satisfeitas é
- A) \(30 \le b\)
- B) \(30 \le b \le 31{,}5\)
- C) \(30 \le b \le 33\)
- D) \(31{,}5 \le b \le 33\)
- E) \(b \le 33\)
Mostrar / esconder solução passo a passo
1) Aplicando a restrição principal
Com \(h=16\), temos \(2h=32\). A condição
\( \lvert 2h + b – 63{,}5 \rvert \le 1{,}5 \)
equivale a
\( 63{,}5 – 1{,}5 \le 2h + b \le 63{,}5 + 1{,}5 \),
isto é,
\( 62 \le 2h + b \le 65 \).
2) Isolando \(b\)
Substituindo \(2h=32\):
\[
62 \le 32 + b \le 65
\;\Rightarrow\;
30 \le b \le 33.
\]
3) Verificando demais condições
A condição \(16 \le h \le 19\) é satisfeita (pois \(h=16\)). Não há outras restrições sobre \(b\) além de ser medida em cm.
Resposta: letra C — \(30 \le b \le 33\).
Mais questões resolvidas — Matemática ENEM 2020
Explore soluções passo a passo:
banco de questões de Matemática do ENEM
.













