Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.
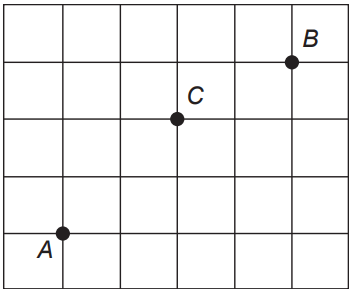
André deseja deslocar-se da sua casa até a casa de Bernardo, sem passar pela casa de Carlos, seguindo ao longo das ruas do condomínio, fazendo sempre deslocamentos para a direita (→) ou para cima (↑), segundo o esquema da figura.
O número de diferentes caminhos que André poderá utilizar para realizar o deslocamento nas condições propostas é
- A) 4
- B) 14
- C) 17
- D) 35
- E) 48
Mostrar / esconder solução passo a passo
1) Total de caminhos A → B (sem restrição)
Do ponto A até B são necessários 4 passos à direita e 3 para cima (observando a malha da figura).
Logo, o total é \(\binom{7}{3}=35\).
2) Caminhos que passam por C
De A até C: 2 à direita e 2 para cima ⇒ \(\binom{4}{2}=6\).
De C até B: 2 à direita e 1 para cima ⇒ \(\binom{3}{1}=3\).
Pelas regras do produto, caminhos via C: \(6\cdot3=18\).
De C até B: 2 à direita e 1 para cima ⇒ \(\binom{3}{1}=3\).
Pelas regras do produto, caminhos via C: \(6\cdot3=18\).
3) Caminhos válidos (evitando C)
\(35-18=\boxed{17}\).
Gabarito: letra C — 17 caminhos.
Veja também — questão anterior do ENEM 2020 Matemática (resolvida)
questão de Matemática do ENEM 2020 resolvida passo a passo
.
Mapas Mentais de Matemática
acessar.
10 eBooks de Matemática
baixar.













