Num octaedro regular, duas faces são consideradas opostas quando não têm nem arestas, nem vértices em comum. Na figura, observa-se um octaedro regular e uma de suas planificações, na qual há uma face colorida na cor cinza escuro e outras quatro faces numeradas.
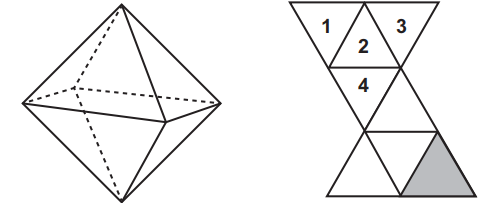
Qual(is) face(s) ficará(ão) oposta(s) à face de cor cinza escuro, quando o octaedro for reconstruído a partir da planificação dada?
- 1, 2, 3 e 4
- 1 e 3
- 1
- 2
- 4
Mostrar / esconder solução passo a passo
1) Ideia-chave
Em um octaedro regular, duas faces opostas não compartilham nem aresta nem vértice. Na planificação dada, a face escura está ligada, por arestas, a algumas faces numeradas; a que for oposta não pode ter nenhuma conexão (nem por aresta, nem por vértice) com a escura após a dobra.
2) Leitura da planificação
Observando a rede, a face 4 é a única que, quando dobramos o sólido, não fica adjacente à face escura e tampouco compartilha vértices com ela. As faces 1, 2 e 3, por sua vez, ficam incidentes (compartilham arestas/vértices) com a face escura.
Logo, a face oposta é 4. Gabarito: letra E.
Página desta questão
ENEM 2021 — Matemática — Questão 10
.
Banco de Questões do ENEM (Matemática)
acessar agora.
Mapas Mentais de Matemática
ver mapas.
10 eBooks de Matemática
baixar eBooks.












