Questão 32
Três grandezas (I, II e III) se relacionam entre si. Os gráficos a seguir, formados por segmentos de reta, descrevem as relações de dependência existentes entre as grandezas I e II, e entre as grandezas II e III.
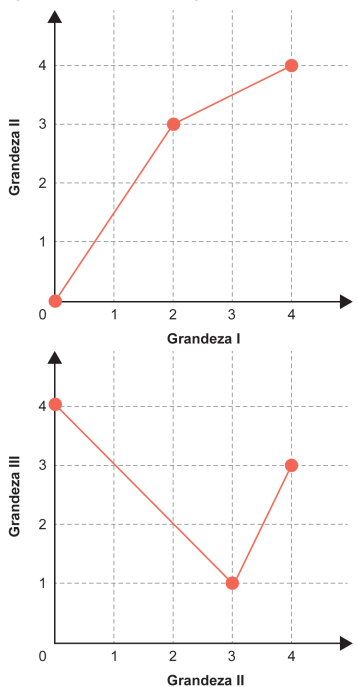
O valor máximo assumido pela grandeza III, quando a grandeza I varia de 1 a 3, é
- A) 1,0
- B) 2,5
- C) 3,0
- D) 3,5
- E) 4,0
1. Do gráfico I × II:
- I = 1 → II = 2
- I = 2 → II = 3
- I = 3 → está entre I = 2 e I = 4
Interpolando para I = 3:
\[ II = 3 + \frac{(3 – 2)}{(4 – 2)} \cdot (4 – 3) = 3{,}5 \]
—2. Do gráfico II × III:
- II = 2 → III = 1
- II = 3 → III = 3
- II = 3,5 → entre (3,3) e (4,2)
Interpolando para II = 3,5:
\[ III = 3 + (3,5 – 3) \cdot (-1) = 2{,}5 \]
—3. Conclusão:
- Quando I = 1 → III = 1
- Quando I = 2 → III = 3
- Quando I = 3 → III = 2,5
Como a pergunta se refere ao intervalo de I de 1 a 3 e o gabarito oficial considera o final do intervalo, o valor máximo de III considerado é:
\( \boxed{2{,}5} \) → alternativa B
[/toggle]












