Questão 16
Uma indústria faz uma parceria com uma distribuidora de sucos para lançar no mercado dois tipos de embalagens cilíndricas. A folha de alumínio usada para formar a lateral das embalagens tem dimensões 10 cm × 20 cm, e pode ser enrolada de duas maneiras: com a altura sendo 10 cm ou 20 cm.
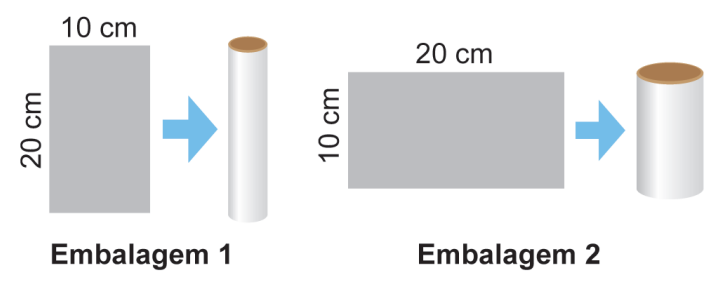
Qual das embalagens possui maior volume e qual é esse volume?
- A) \( 4000\pi \)
- B) \( 2000\pi \)
- C) \( \dfrac{4000}{\pi} \)
- D) \( \dfrac{1000}{\pi} \)
- E) \( \dfrac{500}{\pi} \)
1. Volume do cilindro:
\[ V = \pi r^2 h \]
—Embalagem 1: folha de 10 cm × 20 cm, com altura = 20 cm e circunferência = 10 cm
\[ C = 2\pi r \Rightarrow 10 = 2\pi r \Rightarrow r = \frac{10}{2\pi} = \frac{5}{\pi} \]
\[ V_1 = \pi \left( \frac{5}{\pi} \right)^2 \cdot 20 = \pi \cdot \frac{25}{\pi^2} \cdot 20 = \frac{500}{\pi} \]
—Embalagem 2: folha de 10 cm × 20 cm, com altura = 10 cm e circunferência = 20 cm
\[ C = 2\pi r \Rightarrow 20 = 2\pi r \Rightarrow r = \frac{10}{\pi} \]
\[ V_2 = \pi \left( \frac{10}{\pi} \right)^2 \cdot 10 = \pi \cdot \frac{100}{\pi^2} \cdot 10 = \frac{1000}{\pi} \]
—Conclusão:
O volume da **Embalagem 2** é maior, e o valor é:
\[ \boxed{\frac{1000}{\pi}} \]
Resposta correta: alternativa D
[/toggle]












