Se prepare para o concurso dos Correios resolvendo 10 questões de matemática cuidadosamente selecionadas para ajudá-lo a revisar os principais conteúdos cobrados na prova. Com explicações claras e dicas valiosas, este material é ideal para quem busca reforçar os estudos e aumentar suas chances de aprovação!

01 – Matemática Financeira – Concurso Correios 2011 – Banca CESPE

Em um escritório, a despesa mensal com os salários dos 10 empregados é de R$ 7.600,00. Nesse escritório, alguns empregados recebem, individualmente, R$ 600,00 de salário mensal e os outros, R$ 1.000,00.
A partir das informações do texto, considere que aos empregados que recebem salário mensal de R$ 600,00 seja concedido reajuste salarial de 10%, e aos que recebem salário de R$ 1.000,00, reajuste de 15%. Nesse caso, a despesa mensal do escritório com os salários de seus empregados aumentará entre
A) 7% e 9%.
B) 9% e 11%.
C) 11% e 13%.
D) 13% e 15%.
E) 5% e 7%.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Vamos resolver a questão calculando, passo a passo, o aumento nas despesas com os salários após os reajustes.

1. Definindo variáveis:

• Número de empregados que recebem R$ 600,00: ( x )
• Número de empregados que recebem R$ 1.000,00: ( y )
• Sabemos que há 10 empregados, então:
  
  x + y = 10
  
• A despesa total mensal antes do reajuste é de R$ 7.600,00, ou seja:
  
  600x + 1.000y = 7.600
  

2. Resolvendo o sistema:

Podemos usar o método de substituição. Da equação ( x + y = 10 ), temos:

x = 10 – y

Substituímos ( x ) na equação ( 600x + 1.000y = 7.600 ):

600(10 – y) + 1.000y = 7.600

6.000 – 600y + 1.000y = 7.600

400y = 1.600

y = 4

Logo, 4 empregados recebem R$ 1.000,00 e ( x = 10 – 4 = 6 ) empregados recebem R$ 600,00.

3. Calculando a nova despesa com os salários após o reajuste:

• Reajuste para os empregados que recebem R$ 600,00:
  
  600 x 1,10 = 660
  
  Nova despesa para os 6 empregados: 660 x 6 = 3.960
  
• Reajuste para os empregados que recebem R$ 1.000,00:
  
  1.000 x 1,15 = 1.150
  
  Nova despesa para os 4 empregados: 1.150 x 4 = 4.600

4. Nova despesa total:

Nova despesa total: 3.960 + 4.600 = 8.560

5. Calculando o aumento percentual:

A despesa inicial era de R$ 7.600,00, e a nova despesa é de R$ 8.560,00. O aumento na despesa é:

8.560 – 7.600 = 960

O percentual de aumento é:

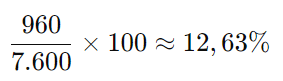
6. Conclusão:

A despesa mensal do escritório com os salários aumentará entre 11% e 13%.

Portanto, a resposta correta é a alternativa C) 11% e 13%.

[/toggle]

02 – Equação do 1° Grau – Concurso Correios 2011 – Banca CESPE

O trajeto de 5 km percorrido por um carteiro é formado por 2 trechos. Sabe-se que os comprimentos desses trechos, em metros, são números diretamente proporcionais a 2 e 3. Nesse caso, a diferença, em metros, entre os comprimentos do maior trecho e do menor trecho é igual a
Alternativas
A) 600.
B) 1.400.
C) 1.200.
D) 1.000.
E) 800.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Vamos resolver o problema considerando que os comprimentos dos dois trechos são diretamente proporcionais a 2 e 3, e que o trajeto total é de 5 km, ou seja, 5.000 metros.

Passos para resolver:

1. Definir as variáveis para os comprimentos dos trechos:

Seja ( x ) o fator de proporcionalidade, então os comprimentos dos trechos são:

• ( 2x ) metros para o menor trecho,
• ( 3x ) metros para o maior trecho.

1. Somar os comprimentos dos dois trechos:

Sabemos que a soma dos dois trechos é igual a 5.000 metros:

2x + 3x = 5.000

5x = 5.000

x = 5.000/5

x = 1.000

3. Calcular os comprimentos dos trechos:

• O menor trecho tem comprimento ( 2x = 2 x 1.000 = 2.000 ) metros,
• O maior trecho tem comprimento ( 3x = 3 x 1.000 = 3.000 ) metros.

3. Calcular a diferença entre os comprimentos:

A diferença entre o maior trecho e o menor trecho é:

3.000 – 2.000 = 1.000 metros

Resposta correta: D) 1.000.

[/toggle]

03 -Estatística – Concurso CORREIOS 2008 – Banca CONSULPLAN

A média aritmética das idades entre os funcionários da Agência Central dos Correios de Recife/PE: Júlio, Adriana, Renato e Otávio é de 24 anos. Se a média de idade dos homens é de 23 anos, qual é a idade de Adriana?

A) 35
B) 32
C) 20
D) 47
E) 27

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Sabemos que a média aritmética das idades de Júlio, Adriana, Renato e Otávio é de 24 anos. Logo, a soma das idades dos quatro funcionários é:

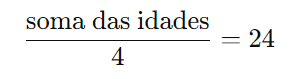
Multiplicando ambos os lados por 4, temos:

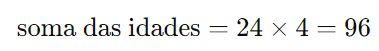
Além disso, a média das idades dos homens (Júlio, Renato e Otávio) é de 23 anos, ou seja, a soma das idades dos três homens é:

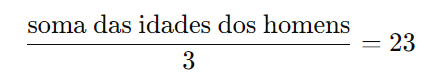
Multiplicando ambos os lados por 3, temos:

Agora, para encontrar a idade de Adriana, subtraímos a soma das idades dos homens da soma total das idades:

Portanto, a idade de Adriana é 27 anos.

A resposta correta é E) 27.

[/toggle]

04 – Inequação Quadrática – Concurso CORREIOS 2008 – Banca CONSULPLAN

Segundo as previsões de um jornal econômico, o PIB anual de um país(y) em bilhões de dólares daqui a x anos poderá ser calculado pela expressão: y = 4/5x² – 8x + 80. Para quais valores de x, o PIB anual desse país ultrapassará 140 bilhões de dólares?

A) x > 15

B) x > 5

C) x < 15

D) x < 5

E) x > 10

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Para resolver o problema, queremos encontrar os valores de ( x ) para os quais o PIB anual ( y ) ultrapassa 140 bilhões de dólares, ou seja, precisamos resolver a desigualdade:

y > 140

A expressão que relaciona o PIB ( y ) ao número de anos ( x ) é dada por:

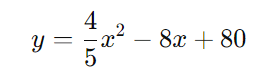
Substituímos ( y > 140 ) na equação:

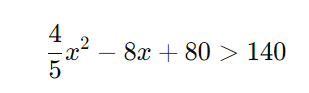
Passo 1: Isolando a equação

Subtraímos 140 de ambos os lados:

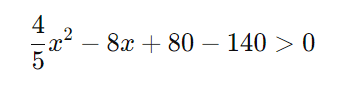
Simplificando:

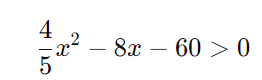
Vamos começar do passo 3, onde temos a equação:4×2−40x−300>04x^2 – 40x – 300 > 04×2−40x−300>0

Passo 3: Dividir por 4

Agora, dividimos toda a equação por 4 para simplificar:

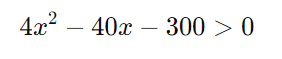
Passo 4: Resolver a equação quadrática

Precisamos encontrar as raízes da equação x² − 10x − 75 = 0. Usamos a fórmula de Bhaskara:

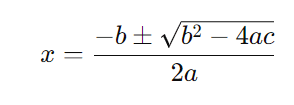
Aqui, a=1, b=−10, e c=−75. Substituímos esses valores na fórmula:

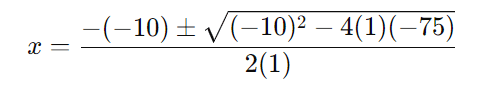
Calculando o discriminante:

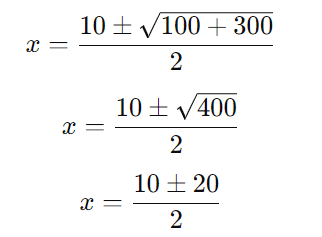
Passo 5: Encontrar as raízes

Agora, calculamos as duas soluções:

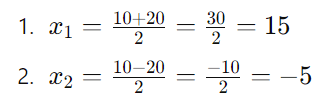
Passo 6: Análise da inequação

A equação x² − 10x − 75 > 0 é positiva fora do intervalo entre as raízes x=−5 e x=15. Portanto, a solução da desigualdade ocorre quando x<−5 ou x>15.

No contexto do problema, onde xxx representa o número de anos no futuro, não faz sentido considerar valores negativos de xxx. Assim, temos:

x>15

Resposta:

A alternativa correta é A) x>15.

[/toggle]

05 – Logaritmo – Concurso CORREIOS 2008 – Banca CONSULPLAN

Sabendo que log₁₀ 2 ≅ 0,3 qual é o menor número natural que verifica a relação 2ⁿ > 10⁴ ?

( ≅: aproximadamente)

A) 11
B) 12
C) 13
D) 14
E) 15

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Vamos resolver a equação (2ⁿ > 10⁴).

Sabemos que ( log 10² ≈ 0,3 ), o que nos dá uma aproximação útil, mas vamos trabalhar com a relação básica diretamente. Precisamos encontrar o menor valor de ( n ) que satisfaça essa desigualdade.

Podemos aplicar o logaritmo para simplificar a desigualdade. Tomando o logaritmo de ambos os lados da equação:

Usando a propriedade dos logaritmos, temos:

Sabemos que ( log(10) = 1 ), e a aproximação para ( log(2) ) é cerca de 0,3 (aproximadamente):

Agora, dividimos ambos os lados por 0,3:

Portanto, o menor número natural que satisfaz a relação ( 2ⁿ > 10⁴ ) é 14.

A resposta correta é D) 14.

[/toggle]

06 – Matemática Financeira – Concurso CORREIOS 2008 – Banca CONSULPLAN

Felipe aplicou uma quantia de R$1.200,00 à taxa de juros simples de 1,5% ao mês durante 1 ano e 4 meses. Passado esse período, ele aplicou o montante produzido e fez uma nova aplicação, à taxa de 1,8% ao mês por 2 meses e 20 dias. Com estas aplicações, quanto Felipe obteve de juros?

A) R$ 1.382,24

B) R$ 359,42

C) R$ 414,72

D) R$ 2.142,72

E) R$ 71,42

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Para resolver essa questão, utilizaremos a fórmula dos juros simples:

Onde:

• ( J ) é o valor dos juros,
• ( C ) é o capital aplicado,
• ( i ) é a taxa de juros,
• ( t ) é o tempo da aplicação.

1ª Aplicação

• Capital inicial (C₁ ): R$ 1.200,00
• Taxa de juros (i₁): 1,5% ao mês = 0,015 ao mês
• Tempo (t₁): 1 ano e 4 meses = 12 + 4 = 16 meses

Calculando os juros da 1ª aplicação:

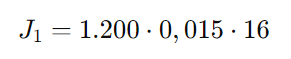
J₁ = 1.200 x 0,24 = R$ 288,00

Montante da 1ª aplicação:

M₁ = C₁ + J₁ = 1.200 + 288 = R$ 1.488,00

2ª Aplicação

Agora, o montante da 1ª aplicação (( M_1 )) é aplicado a uma nova taxa de juros.

• Capital (C₂): R$ 1.488,00
• Taxa de juros (i₂): 1,8% ao mês = 0,018 ao mês
• Tempo (t₂): 2 meses e 20 dias = 2 + 20/30 = 2 + 0,67 = 2,67 meses

Calculando os juros da 2ª aplicação:

J₂ = 1.488 .0,018 . 2,67

J2 = 1.488 .0,04806 = R$ 71,42

Total de juros

Somando os juros das duas aplicações:

J_total = J₁ + J₂ = 288 + 71,42 = R$ 359,42

Assim, a alternativa correta é:

B) R$ 359,42

[/toggle]

07 – Porcentagem – Concurso Correios 2011 – Banca CESPE

Uma equipe de conferentes analisou os registros de determinados documentos. Todos os membros dessa equipe trabalham com a mesma eficiência, e 3 deles analisaram 60% de todo o material.

A partir das informações do texto, infere-se que a quantidade de conferentes da equipe é igual a

A) 6.

B) 7.

C) 8.

D) 9.

E) 5.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Vamos resolver a questão com base nas informações fornecidas.

• Sabemos que 3 conferentes analisaram 60% do material.
• A questão também afirma que todos os conferentes têm a mesma eficiência, ou seja, cada um analisaria a mesma quantidade proporcional de material.

Se 3 conferentes analisam 60% do material, podemos concluir que:

1. A eficiência de cada conferente é a mesma. Logo, a porcentagem de material que cada conferente analisa pode ser dividida de forma proporcional.
2. Queremos descobrir a quantidade total de conferentes (vamos chamar esse valor de ( x )).

Agora, vamos montar uma regra de três simples:

• 3 conferentes analisam 60% do material.
• ( x ) conferentes analisam 100% do material.

Montando a regra de três:

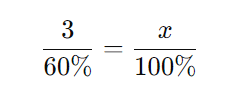
Agora, resolvemos a equação:

Multiplicando em cruz:

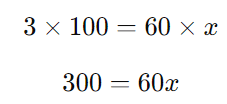
Dividindo ambos os lados por 60:

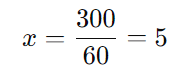
Portanto, a quantidade total de conferentes é 5.

A resposta correta é a alternativa E) 5.

[/toggle]

08 – Probabilidade – Concurso CORREIOS 2008 – Banca CONSULPLAN

Na Agência dos Correios de uma certa cidade trabalham 20 funcionários. Sabe-se que 12 desses funcionários jogam futebol, 8 jogam vôlei e 5 jogam futebol e vôlei. Escolhendo ao acaso um dos funcionários, qual a probabilidade dele não praticar nenhum desses esportes?

A) 12%
B) 5%
C) 25%
D) 50%
E) 75%

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Para resolver essa questão, vamos usar a fórmula do princípio da inclusão e exclusão.

Passo 1: Definir os conjuntos

• ( A ): conjunto de funcionários que jogam futebol.
• ( B ): conjunto de funcionários que jogam vôlei.
• ( |A| = 12 ) (12 funcionários jogam futebol).
• ( |B| = 8 ) (8 funcionários jogam vôlei).
• ( |A ∩ B| = 5 ) (5 funcionários jogam os dois esportes).

Passo 2: Calcular o total de funcionários que praticam pelo menos um dos esportes

A fórmula do princípio da inclusão e exclusão é:

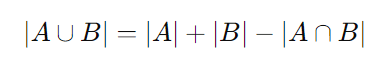
Substituindo os valores:

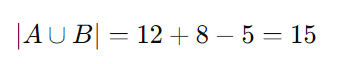
Então, 15 funcionários jogam futebol, vôlei ou ambos.

Passo 3: Calcular quantos funcionários não jogam nenhum dos esportes

O total de funcionários na agência é 20. Logo, o número de funcionários que não jogam nenhum dos esportes é:

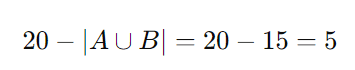
Passo 4: Calcular a probabilidade

A probabilidade de escolher um funcionário que não joga nenhum dos esportes é:

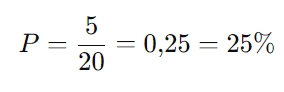
Resposta correta:

C) 25%

[/toggle]

09 – Raciocínio Lógico– Concurso CORREIOS 2017 – Banca IADES

A maioria dos países, incluindo o Brasil, adota as dimensões dos tamanhos de papel de acordo com a série A, conforme definido pela ISO 216.

A imagem apresentada, que contém os tamanhos de papel da série A, oferece uma representação visual de como os tamanhos relacionam-se entre si – por exemplo, A5 é metade do tamanho A4 e A2 é metade do tamanho A1.

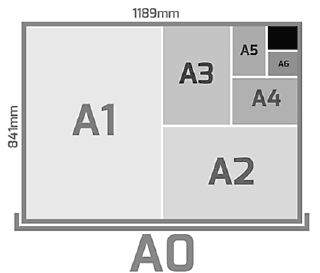
Com base nessas informações, quantas folhas de papel A6 são necessárias para formar uma folha de papel A2?

A) 2
B) 16
C) 8
D) 4
E) 32

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Para resolver essa questão, vamos usar o conceito de que cada tamanho da série A é obtido dividindo o tamanho anterior ao meio.

Passo 1: Relação entre os tamanhos da série A

Sabemos que:

• Uma folha de A6 é metade de uma folha de A5.
• Uma folha de A5 é metade de uma folha de A4.
• Uma folha de A4 é metade de uma folha de A3.
• Uma folha de A3 é metade de uma folha de A2.

Passo 2: Determinar quantas folhas de A6 formam uma folha de A2

Vamos seguir a lógica de divisões:

• Uma folha de A2 é composta por 2 folhas de A3.
• Cada folha de A3 é composta por 2 folhas de A4, ou seja, uma folha de A2 tem 4 folhas de A4.
• Cada folha de A4 é composta por 2 folhas de A5, ou seja, uma folha de A2 tem 8 folhas de A5.
• Cada folha de A5 é composta por 2 folhas de A6, ou seja, uma folha de A2 tem 16 folhas de A6.

Resposta:

Portanto, são necessárias 16 folhas de A6 para formar uma folha de A2.

A resposta correta é B) 16.

[/toggle]

10 – Unidade de Medida – Concurso Correios 2008 – Banca CONSULPLAN

Uma torneira mal fechada goteja cem vezes a cada 5 minutos. Admitindo-se que todas as gotas têm a capacidade de 3ml, a quantidade de água que vaza por hora é:

A) menor que 1 litro.

B) maior que 1 litro.

C) igual a 1 litro.

D) maior que 10 litros.

E) menor que 10 litros.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Vamos calcular a quantidade de água que vaza por hora.

Sabemos que:

• A torneira goteja 100 vezes a cada 5 minutos.
• Cada gota tem 3 ml.

Primeiro, precisamos descobrir quantas gotas caem em uma hora.

Agora, vamos calcular o volume total de água que vaza por hora. Sabemos que cada gota tem 3 ml, então:

Convertendo para litros (1 litro = 1000 ml):

Portanto, a quantidade de água que vaza por hora é 3,6 litros.

A resposta correta é:

B) maior que 1 litro.

[/toggle]