Prepare-se para o concurso dos Correios com um conjunto de questões essenciais para reforçar seu conhecimento em matemática. Deixe a insegurança de lado e pratique com questões que abrangem os tópicos mais cobrados, desde operações básicas até problemas envolvendo lógica e proporções. Aprenda a resolver cada questão de forma eficiente e descubra dicas para maximizar seu desempenho na prova! 📈💡 Conquiste sua vaga com confiança!
01 – (CESPE – 2011 – Correios) O Programa Nacional do Livro Didático e o Programa Nacional do Livro Didático para o Ensino Médio são realizados pela ECT em parceria com o Fundo Nacional de Desenvolvimento da Educação. A operação consiste na entrega, todos os anos, de 100 milhões de livros didáticos a escolas públicas de ensino fundamental e médio de todo o Brasil, volume equivalente à metade de toda a produção gráfica do Brasil. Para a distribuição desses livros são realizadas viagens de carretas das editoras para os centros de tratamento da empresa instalados em pontos estratégicos do país. Nessas unidades, as encomendas são tratadas e, depois, entregues nas escolas.
Considerando que 7⁄40 e 13% dos livros didáticos sejam distribuídos, respectivamente, para as regiões Nordeste e Norte, então a quantidade, em milhões, de livros didáticos destinada a essas duas regiões pelos programas mencionados no texto é
A) superior a 15 e inferior a 25.
B) superior a 25 e inferior a 35.
C) superior a 35 e inferior a 45.
D) superior a 45.
E) inferior a 15.
Ver Solução
Para resolver essa questão, precisamos calcular a quantidade de livros didáticos destinada às regiões Nordeste e Norte, considerando os percentuais dados:
- Total de livros distribuídos: 100 milhões.
- Para a região Nordeste: 7/40 do total.
- Para a região Norte: 13% do total.
Passo 1: Calculando para a Região Nordeste
Para encontrar a quantidade de livros destinados ao Nordeste, multiplicamos o total de livros por 7/40:
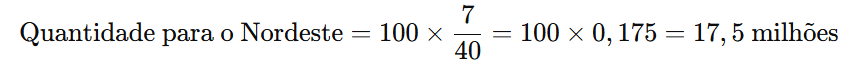
Passo 2: Calculando para a Região Norte
Para encontrar a quantidade de livros destinados ao Norte, multiplicamos o total de livros por 13% (ou 0,13):
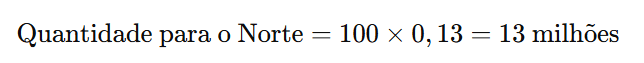
Passo 3: Somando as Quantidades
A quantidade total de livros destinada às duas regiões é a soma dos valores calculados:
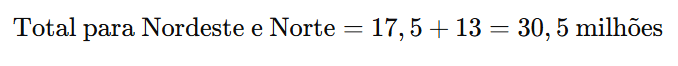
Conclusão
A quantidade total de livros destinada às regiões Nordeste e Norte é 30,5 milhões, o que se enquadra na opção:
B) superior a 25 e inferior a 35.
02 – (CESPE – 2011 – Correios) A primeira unidade do novo modelo de agência franqueada dos Correios foi inaugurada em 10/2/2011, em Ourinhos, no interior do estado de São Paulo. A nova agência, com 200 metros quadrados de área, situa-se na Vila Recreio.
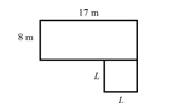
Considerando que essa nova agência seja composta de 2 salas, uma retangular, com lados medindo 17 m e 8 m e outra, quadrada, com lados medindo L metros, conforme ilustrado na figura acima, é correto afirmar que o valor de L é
A) superior a 5 e inferior a 7.
B) superior a 7 e inferior a 9.
C) superior a 9.
D) inferior a 3.
E) superior a 3 e inferior a 5.
Ver Solução
Análise da Figura
Na imagem, temos:
- Uma sala retangular com dimensões de 17 metros por 8 metros.
- Uma sala quadrada anexada à sala retangular, com lados medindo ( L ) metros.
Passo 1: Calcular a Área da Sala Retangular
A área da sala retangular é calculada multiplicando o comprimento pela largura:
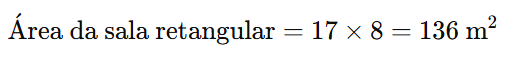
Passo 2: Determinar a Área da Sala Quadrada
A área total da agência é de 200 m². Subtraindo a área da sala retangular, encontramos a área da sala quadrada:
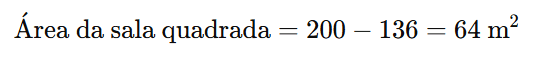
Passo 3: Calcular o Valor de ( L )
Como a área da sala quadrada é ( L2 ), temos:
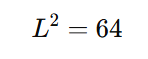
Resolvendo para ( L ):
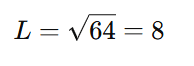
Conclusão
O valor de ( L ) é 8, o que corresponde à alternativa:
B) superior a 7 e inferior a 9.
03 – (CESPE – 2011 – Correios) As remunerações brutas mensais — isto é, sem qualquer desconto — dos empregados de determinada empresa são calculadas com base na soma das seguintes quantidades:
- salário fixo, no valor de R$ 2.400,00, correspondente a 160 horas trabalhadas no mês;
- horas extras, definidas como a remuneração correspondente à quantidade de horas e(ou) fração de hora que ultrapassar as 160 horas exigidas, multiplicada pelo valor de cada hora completa, que é igual a R$ 15,00.
Com base nessa situação hipotética e considerando-se que, em determinado mês, a remuneração bruta de um empregado dessa empresa foi igual a R$ 2.750,00, é correto afirmar que, nesse mês, esse empregado trabalhou durante 183 horas e
A) 20 minutos.
B) 25 minutos.
C) 30 minutos.
D) 10 minutos.
E) 15 minutos.
Ver Solução
Para resolver essa questão, vamos entender a composição da remuneração bruta do empregado e calcular a quantidade de horas extras trabalhadas para que ele tenha recebido um valor bruto de R$ 2.750,00.
Dados do Problema
- Salário fixo: R$ 2.400,00 para 160 horas de trabalho no mês.
- Valor da hora extra: R$ 15,00 por hora ou fração de hora além das 160 horas.
- Remuneração bruta do mês: R$ 2.750,00.
Passo 1: Calcular o Valor das Horas Extras
A remuneração bruta é a soma do salário fixo com o valor das horas extras:
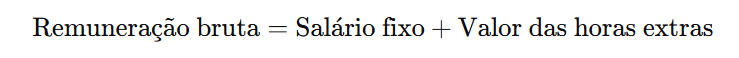
Substituindo os valores, temos:
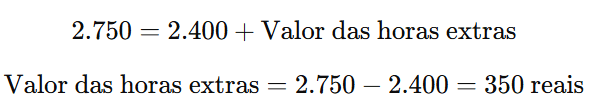
Passo 2: Determinar a Quantidade de Horas Extras
Como cada hora extra vale R$ 15,00, a quantidade de horas extras ( H ) pode ser calculada por:
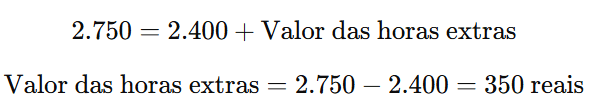
A parte inteira é 23 horas e a parte decimal, 0,333… de uma hora.
Passo 3: Converter a Fração de Hora em Minutos
Para converter 0,333… de uma hora em minutos, multiplicamos por 60:
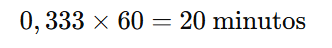
Conclusão
O empregado trabalhou 183 horas e 20 minutos, o que corresponde à alternativa:
A) 20 minutos.
04 – (CESPE – 2011 – Correios) Sabendo-se que todos os ângulos dos vértices do terreno ilustrado na figura acima medem 90o e que o metro quadrado do terreno custa R$ 120,00, é correto afirmar que o preço desse terreno é
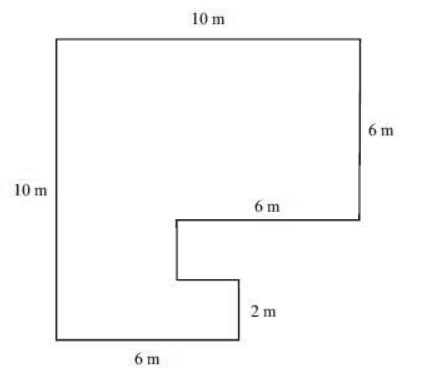
A) superior a R$ 9.900,00 e inferior a R$ 10.100,00.
B) superior a R$ 10.100,00.
C) inferior a R$ 9.500,00.
D) superior a R$ 9.500,00 e inferior a R$ 9.700,00.
E) superior a R$ 9.700,00 e inferior a R$ 9.900,00.
Ver Solução
A questão trata de geometria plana.
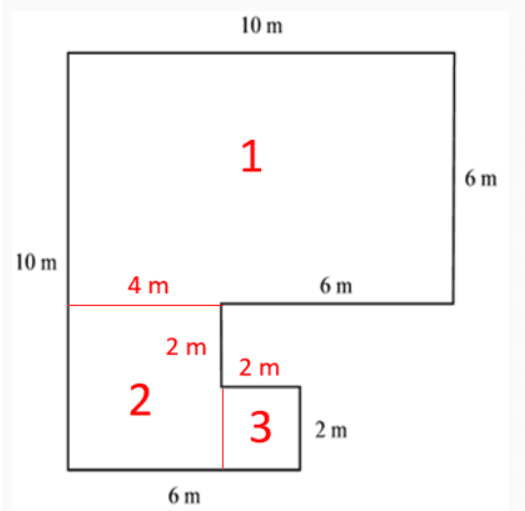
A = A1 + A2 + A3
A = 10 × 6 + 4 × (2 + 2) + 2 × 2
A = 60 + 16 + 4 = 80 m²
Preço = 80 m² × R$120,00 / m²
Preço = R$9.600,00
Gabarito: LETRA D.
05 – (CESPE – 2011 – Correios) Considere que sejam cobrados R$ 5,00 para o envio de uma carta comercial simples e uma carta comercial registrada, ambas de até 20 g, e R$ 11,10 para o envio de 3 cartas comerciais simples e 2 registradas, todas de até 20 g. Nessa situação, a diferença entre o preço cobrado para o envio de uma carta comercial registrada e o cobrado para o envio de uma carta comercial simples, ambas de até 20 g, é de
A) R$ 2,60.
B) R$ 2,70.
C) R$ 2,80.
D) R$ 2,90.
E) R$ 2,50.
Ver Solução
Vamos resolver o problema considerando as informações dadas:
- Seja:
- ( x ): o preço do envio de uma carta comercial simples.
- ( y ): o preço do envio de uma carta comercial registrada.
- De acordo com o enunciado:
- O envio de uma carta comercial simples e uma registrada custa R$ 5,00, então:
x + y = 5 - O envio de 3 cartas comerciais simples e 2 registradas custa R$ 11,10, então:
3x + 2y = 11,10
- Agora, vamos resolver esse sistema de equações.
Passo 1: Resolver o sistema de equações
A primeira equação é:
x + y = 5
Portanto, ( y = 5 – x ).
Substituindo ( y ) na segunda equação:
3x + 2(5 – x) = 11,10
3x + 10 – 2x = 11,10
x = 11,10 – 10
x = 1,10
Agora que sabemos que ( x = 1,10 ), substituímos esse valor na primeira equação para encontrar ( y ):
1,10 + y = 5
y = 5 – 1,10
y = 3,90
Passo 2: Calcular a diferença entre ( y ) e ( x )
A diferença entre o preço da carta registrada e o da carta simples é:
y – x = 3,90 – 1,10 = 2,80
Portanto, a resposta correta é:
C) R$ 2,80.
06 – (CESPE – 2011 – Correios) Considere que, em um investimento em caderneta de poupança, a taxa de juros seja de 0,6% ao mês. Nesse caso, se uma pessoa depositar R$ 1.000,00 em uma conta de poupança no dia 1º/6/2011 e não fizer nenhuma retirada, o montante, no aniversário de dois meses desse depósito, será
A) superior a R$ 1.014,00 e inferior a R$ 1.015,00.
B) superior a R$ 1.015,00 e inferior a R$ 1.016,00.
C) superior a R$ 1.016,00.
D) inferior a R$ 1.013,00.
E) superior a R$ 1.013,00 e inferior a R$ 1.014,00.
Ver Solução
Para calcular o montante após dois meses com uma taxa de juros de 0,6% ao mês, usaremos a fórmula do montante para juros compostos:
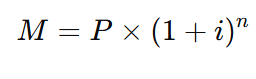
onde:
- ( M ) é o montante final,
- ( P ) é o capital inicial (R$ 1.000,00),
- ( i ) é a taxa de juros mensal (0,6% ou 0,006 em decimal),
- ( n ) é o número de períodos (2 meses).
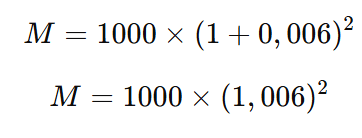
Agora vamos calcular isso:
O montante após dois meses será aproximadamente R$ 1.012,04.
Portanto, a resposta correta é:
D) inferior a R$ 1.013,00.
07 – (CESPE – 2011 – Correios) Vários jornais e revistas anunciaram, nos últimos meses, que o preço do quilo de picanha, corte preferido para o preparo de um bom churrasco, subiu 42%.
Nesse caso, se um consumidor de picanha decidir manter o mesmo gasto mensal com a compra desse alimento, ele deverá diminuir o consumo em
A) mais de 40% e menos de 44%.
B) mais de 44% e menos de 48%.
C) mais de 28% e menos de 32%.
D) mais de 32% e menos de 36%.
E) mais de 36% e menos de 40%.
Ver Solução
Para resolver esse problema, vamos entender a relação entre o aumento do preço e a quantidade que o consumidor poderá comprar mantendo o mesmo orçamento.
Se o preço subiu 42%, o novo preço é 142% do preço original (ou 1,42 vezes o preço original).
Seja:
- ( q ): a quantidade original de picanha que o consumidor comprava antes do aumento.
- ( Q ): a nova quantidade de picanha que o consumidor pode comprar após o aumento, mantendo o mesmo gasto.
A relação entre a quantidade original e a nova quantidade é inversamente proporcional ao aumento do preço. Assim, temos:
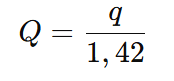
A redução percentual no consumo é dada por:
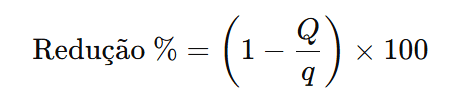
Substituindo ( Q ) na fórmula acima, obtemos:
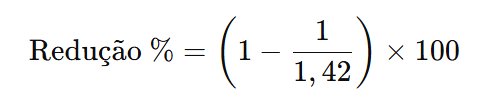
Vou calcular isso para encontrar a resposta.
A redução necessária no consumo para manter o mesmo gasto será aproximadamente 29,58%.
Portanto, a resposta correta é:
C) mais de 28% e menos de 32%.
08 – (CESPE – 2011 – Correios) Na compra de 2 frascos de tira-manchas, cada um deles ao custo de R$ 9,00; 6 frascos de limpador multiuso, cada um deles ao custo de R$ 2,00; 4 litros de desinfetante, cada um deles ao custo de R$ 1,50; e de 6 unidades de esponja dupla face, cada uma delas ao custo de R$ 2,00; um cliente pagou com 3 notas de R$ 20,00, tendo recebido R$ 19,20 de troco.
Nesse caso, o cliente recebeu desconto de
Alternativas
A) 13%.
B) 14%.
C) 15%.
D) 16%.
E) 12%.
Ver Solução
Primeiro, vamos calcular o valor total da compra sem desconto, somando os valores de cada item:
- Tira-manchas: 2 frascos a R$ 9,00 cada.
2 × 9 = 18 reais - Limpador multiuso: 6 frascos a R$ 2,00 cada.
6 × 2 = 12 reais - Desinfetante: 4 litros a R$ 1,50 cada.
4 × 1,50 = 6 reais - Esponja dupla face: 6 unidades a R$ 2,00 cada.
6 × 2 = 12 reais
Somando todos os itens:
18 + 12 + 6 + 12 = 48 reais
Agora, o cliente pagou com 3 notas de R$ 20,00 (total de R$ 60,00) e recebeu R$ 19,20 de troco. Então, ele pagou:
60 – 19,20 = 40,80 reais
Para calcular o desconto, vamos encontrar a diferença entre o valor total (R$ 48,00) e o valor pago (R$ 40,80):
Desconto = 48 – 40,80 = 7,20 reais
Agora, calculamos a porcentagem de desconto em relação ao valor total:
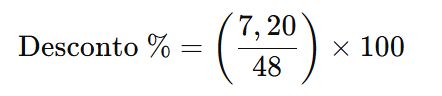
Vou calcular isso para encontrar o resultado.
O desconto concedido foi de aproximadamente 15%.
Portanto, a resposta correta é:
C) 15%.
09 – (CESPE – 2011 – Correios) Em determinado dia, todas as correspondências recebidas na agência dos Correios da cidade Alfa destinavam-se apenas a moradores dos bairros X, Y e Z. Ao bairro X foi destinada metade das correspondências recebidas na agência menos 30 correspondências; ao bairro Y foi destinada a terça parte das correspondências restantes, isto é, depois de retiradas as do bairro X, e mais 70 correspondências; o bairro Z recebeu 180 correspondências.
O total de correspondências recebidas, nesse dia, na agência dos Correios da cidade Alfa foi
A) superior a 680 e inferior a 700.
B) superior a 700 e inferior a 720.
C) superior a 720.
D) inferior a 660.
E) superior a 660 e inferior a 680.
Ver Solução
A resposta completa para a questão é a seguinte:
Seja ( T ) o total de correspondências recebidas na agência dos Correios.
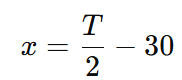
As correspondências destinadas ao bairro Y foram a terça parte das correspondências restantes, após retirar as destinadas ao bairro X, mais 70:
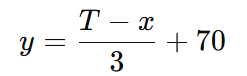
As correspondências destinadas ao bairro Z foram 180:
z = 180
Assim, o total de correspondências é dado por:
T = x + y + z
Substituindo as expressões de ( x ) e ( y ):
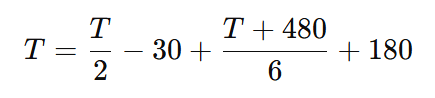
Multiplicando toda a equação por 6 para eliminar as frações:
3T – 180 + T + 480 + 1080 = 6T
Simplificando a expressão:
2T = 1380
Dividindo ambos os lados por 2:
T = 690
Portanto, o total de correspondências recebidas na agência dos Correios da cidade Alfa foi de 690, que se enquadra na opção:
A) superior a 680 e inferior a 700.
10 – (CESPE – 2011 – Correios)
Essa enquete está representada no diagrama retangular de 12 cm de altura, ilustrado abaixo, em que x corresponde ao comprimento da base do retângulo que representa os entrevistados que responderam sim à pergunta; o comprimento da base do retângulo correspondente aos entrevistados que responderam não à pergunta é igual a 4 cm.
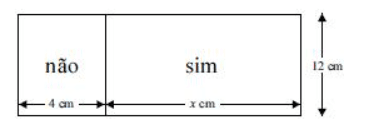
Com base nesses dados, é correto afirmar que o valor de x é
A) superior a 26 e inferior a 29.
B) superior a 29.
C) inferior a 20.
D) superior a 20 e inferior a 23.
E) superior a 23 e inferior a 26.
Ver Solução
Para resolver essa questão, precisamos usar a proporção fornecida para calcular o valor de ( x ), que representa o comprimento da base do retângulo correspondente aos entrevistados que responderam “sim”.
Os dados fornecidos são:
- 84% das pessoas responderam “sim”.
- 16% das pessoas responderam “não”.
- A base do retângulo para “não” mede 4 cm.
Podemos configurar uma proporção entre as bases dos retângulos, usando as porcentagens. Vamos calcular:
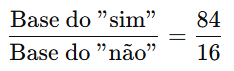
Então, temos:
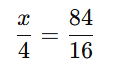
Resolvendo essa equação para ( x ):
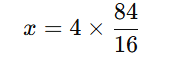
Calculando, teremos o valor de ( x ).
O valor de ( x ) é 21 cm. Portanto, a alternativa correta é:
D) superior a 20 e inferior a 23.
Lista Para o Concurso dos Correios 1
Lista Para o Concurso dos Correios 1
Lista Para o Concurso dos Correios 1
