O que é uma Matriz Coluna?

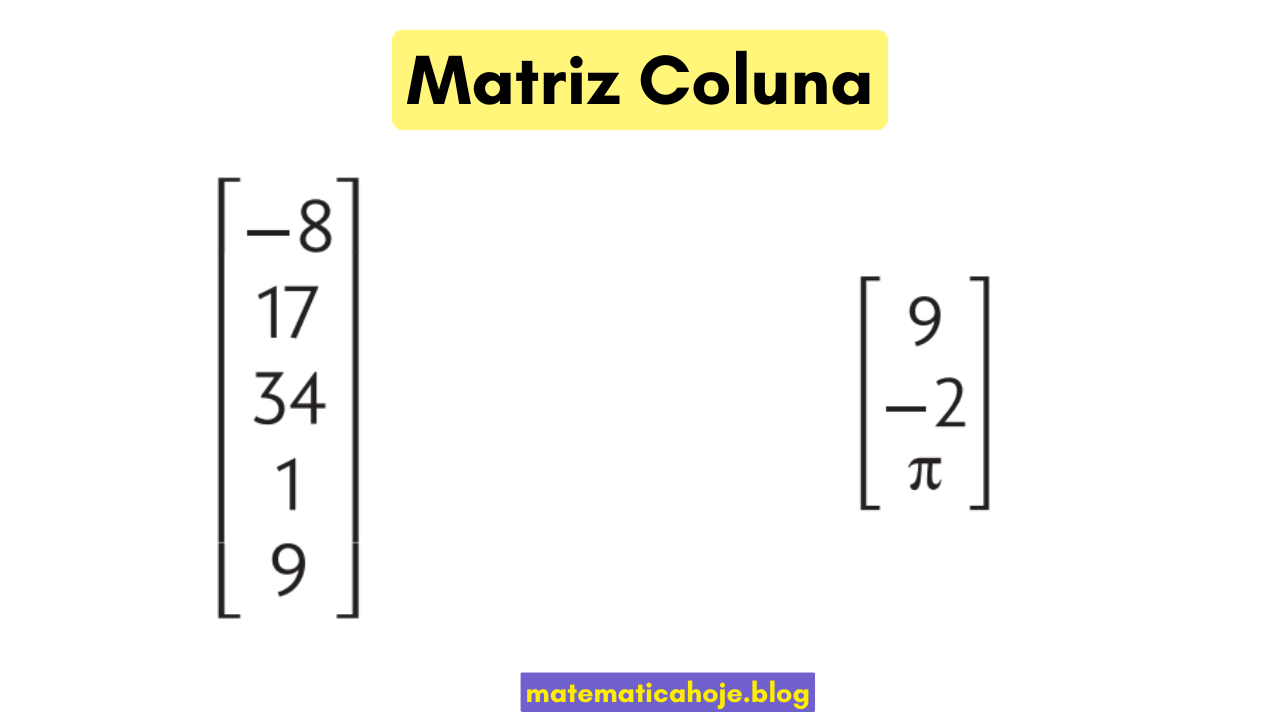
Chamamos de matriz coluna toda matriz com \(m\) linhas e apenas uma coluna. Seu formato é \(m \times 1\). Exemplos:

C = ⎡ -8 ⎤
    ⎢ 17 ⎥
    ⎢ 34 ⎥   → 5 × 1
    ⎢  1 ⎥
    ⎣  9 ⎦

D = ⎡ 9 ⎤
    ⎢-2 ⎥   → 3 × 1
    ⎣ π ⎦

Propriedades e observações

• Uma matriz coluna pode ser vista como um vetor coluna.
• A soma de duas matrizes coluna \(m\times 1\) é outra matriz coluna \(m\times 1\).
• A multiplicação por escalar mantém o formato \(m\times 1\).
• O produto \(L\cdot C\) entre uma matriz linha \(1\times n\) e uma coluna \(n\times 1\) é um escalar (1×1).
• O produto externo \(C\cdot L\) (coluna \(m\times 1\) por linha \(1\times n\)) resulta em uma matriz \(m\times n\).

Exemplos rápidos

1) Soma: \(\begin{bmatrix}2\\-1\\4\end{bmatrix}+\begin{bmatrix}5\\3\\0\end{bmatrix}=\begin{bmatrix}7\\2\\4\end{bmatrix}\).

2) Produto por escalar: \(-2\cdot\begin{bmatrix}4\\0\\-1\end{bmatrix}=\begin{bmatrix}-8\\0\\2\end{bmatrix}\).

3) Produto externo: \(\begin{bmatrix}2\\-1\end{bmatrix}\cdot[\,3\ \ 4\,]=\begin{bmatrix}6&8\\-3&-4\end{bmatrix}\).

Exercícios (múltipla escolha)

1) Qual é a ordem de \(C=\begin{bmatrix}-8\\17\\34\\1\\9\end{bmatrix}\)?

1. \(1\times 5\)
2. \(5\times 1\)
3. \(5\times 5\)
4. \(3\times 1\)

2) Se \(C_1=\begin{bmatrix}4\\0\\-1\end{bmatrix}\) e \(C_2=\begin{bmatrix}-2\\3\\5\end{bmatrix}\), então \(C_1+C_2\) é:

1. \(\begin{bmatrix}2\\3\\4\end{bmatrix}\)
2. \(\begin{bmatrix}6\\3\\4\end{bmatrix}\)
3. \(\begin{bmatrix}2\\3\\-6\end{bmatrix}\)
4. \(\begin{bmatrix}2\\-3\\6\end{bmatrix}\)

3) Seja \(C=\begin{bmatrix}1\\-2\\4\\3\end{bmatrix}\). O produto por \(-2\) é:

1. \(\begin{bmatrix}-2\\4\\-8\\-6\end{bmatrix}\)
2. \(\begin{bmatrix}2\\-4\\8\\6\end{bmatrix}\)
3. \(\begin{bmatrix}-2\\-4\\8\\6\end{bmatrix}\)
4. \(\begin{bmatrix}-2\\4\\8\\-6\end{bmatrix}\)

4) Seja \(L=[\,4\ \ 0\ \ 5\,]\) (matriz linha \(1\times 3\)) e \(C=\begin{bmatrix}1\\2\\-3\end{bmatrix}\) (coluna \(3\times 1\)). Calcule \(LC\).

1. \(-7\)
2. \(-11\)
3. \(11\)
4. \(7\)

5) Dadas \(C=\begin{bmatrix}2\\-1\end{bmatrix}\) e \(L=[\,3\ \ 4\,]\), o produto externo \(CL\) é:

1. \(\begin{bmatrix}6&8\\-3&-4\end{bmatrix}\)
2. \(\begin{bmatrix}6\\8\end{bmatrix}\)
3. \(\begin{bmatrix}1\end{bmatrix}\)
4. \(\begin{bmatrix}3&4\\2&-1\end{bmatrix}\)

6) Para que o produto \(M\cdot C\) esteja definido, onde \(C\) é \(n\times1\), a ordem de \(M\) deve ser:

1. \(1\times n\)
2. \(n\times 1\)
3. \(m\times n\)
4. \(n\times m\)

Leituras relacionadas

Para seguir estudando matrizes: Matriz Linha, Matriz Triangular e uma revisão com Banco de Questões.