Matriz Triangular
Definição, tipos, propriedades, exemplo resolvido e exercícios com gabarito.
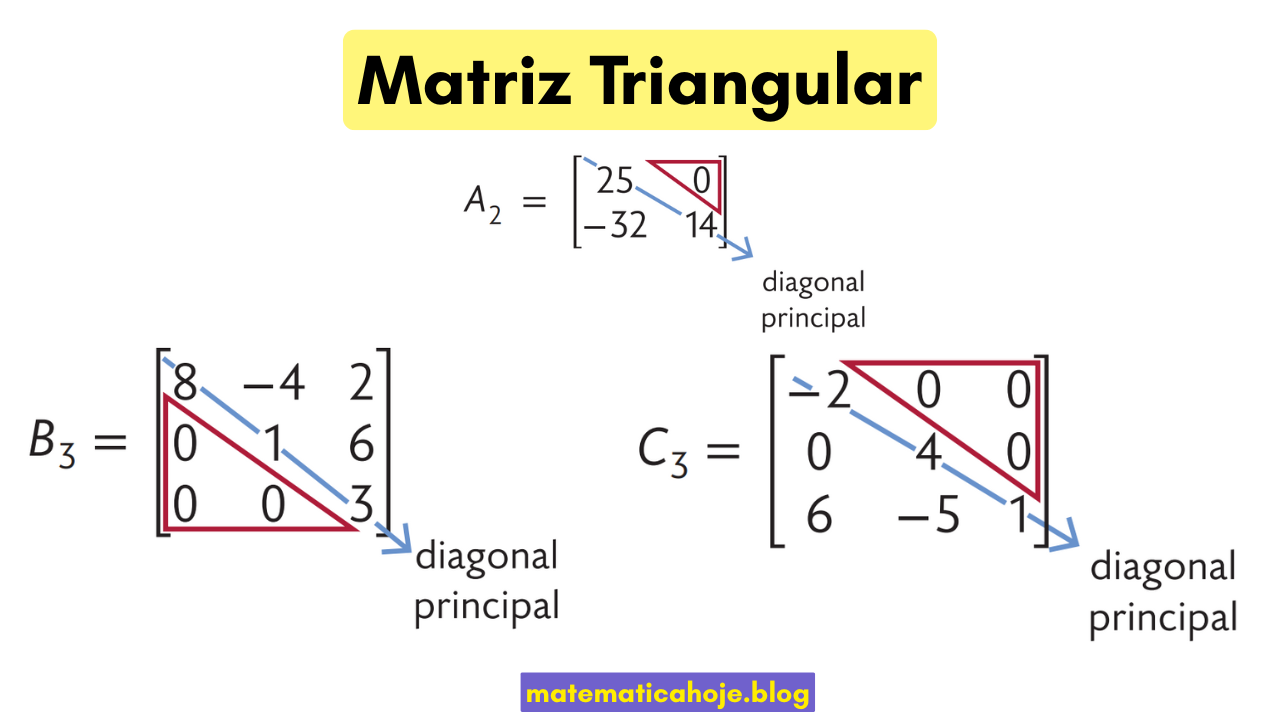
O que é uma Matriz Triangular?
Uma matriz quadrada \(n \times n\) é triangular quando todos os elementos acima ou abaixo da diagonal principal são zeros.
- Triangular superior: \(a_{ij}=0\) para \(i>j\) (abaixo da diagonal).
- Triangular inferior: \(a_{ij}=0\) para \(i<j\) (acima da diagonal).
\(\displaystyle \det(A)=\prod_{k=1}^{n} a_{kk}\) (produto dos elementos da diagonal principal).
Aprofunde com o Banco de Questões e os Mapas Mentais.
Exemplo rápido
M = [ 3 2 5 ] [ 0 4 1 ] [ 0 0 6 ]
\(\det(M)=3\cdot 4 \cdot 6=72\).
Se \(U\) e \(V\) são triangulares superiores (mesma ordem), então \(U+V\) e \(UV\) também são triangulares superiores.
Exercícios de Múltipla Escolha
1) Considere \(A=\begin{bmatrix} 7 & -3 & 2 \\ 0 & 5 & 1 \\ 0 & 0 & -4 \end{bmatrix}\). A matriz é:
- Triangular inferior
- Triangular superior
- Diagonal
- Simétrica
Mostrar solução
2) Para \(B=\begin{bmatrix} 2 & 0 & 0 \\ -1 & 3 & 0 \\ 4 & 5 & -2 \end{bmatrix}\), calcule \(\det(B)\).
- \(-12\)
- \(12\)
- \(-6\)
- \(6\)
Mostrar solução
3) Se \(U\) e \(V\) são \(3\times 3\) triangulares superiores, então \(UV\) é:
- Triangular inferior
- Triangular superior
- Diagonal
- Nenhuma das anteriores
Mostrar solução
4) Seja \(C=\begin{bmatrix} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{bmatrix}\). Escolha a verdadeira:
- \(\det(C)=a+d+f\)
- \(\det(C)=adf\)
- \(\det(C)=af\)
- \(\det(C)=bc+ef\)
Mostrar solução
5) Dadas \(U=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 0 & 0 & 6 \end{bmatrix}\) e \(V=\begin{bmatrix} 2 & 1 & 0 \\ 0 & 3 & -2 \\ 0 & 0 & 5 \end{bmatrix}\), então \(\det(UV)\) vale:
- \( (1\cdot4\cdot6) + (2\cdot3\cdot5) \)
- \( \det(U)+\det(V) \)
- \( \det(U)\cdot\det(V) \)
- \( 0 \)
Mostrar solução
6) Qual condição garante que uma matriz triangular é invertível?
- Ter pelo menos um elemento não nulo fora da diagonal
- Ser simétrica
- Todos os elementos da diagonal principal serem não nulos
- Somar 1 aos elementos da última coluna
Mostrar solução
Materiais Recomendados
Sugestões de leitura: Triângulo de Pascal, Operações com Frações, Equação do 2º grau.





















