Medianas
Em geometria, uma mediana de um triângulo é um segmento de reta que une um vértice ao ponto médio do lado oposto. Cada triângulo possui três medianas, uma a partir de cada vértice, e todas elas se encontram em um único ponto, independentemente do tipo de triângulo.
Num triângulo ABC, marquemos M1 , ponto médio do lado BC.
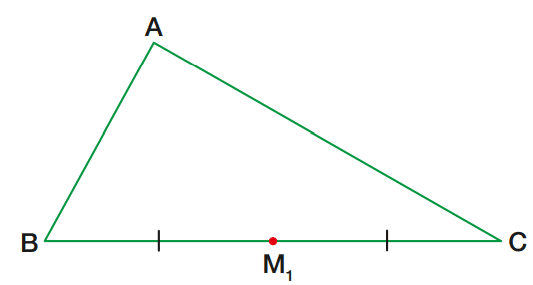
Tracemos o segmento AM1:
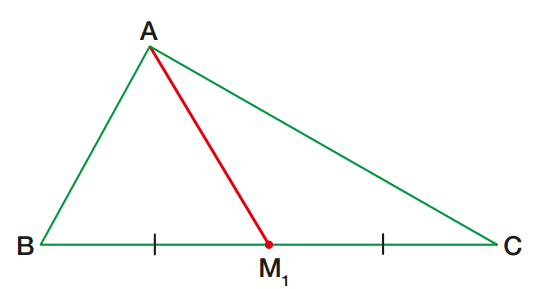
O segmento AM1 é uma mediana do triângulo ABC.
Mediana de um triângulo é um segmento com extremidades num vértice e no ponto médio do lado oposto.
Baricentro
O baricentro é o ponto de encontro das três medianas de um triângulo. Ele também é chamado de centro de gravidade ou centroide. O baricentro divide cada mediana em uma razão de 2:1, ou seja, a distância entre o vértice e o baricentro é o dobro da distância entre o baricentro e o ponto médio do lado oposto.
Em termos práticos, o baricentro é o ponto onde, se o triângulo fosse uma placa de material uniforme, ele poderia ser equilibrado.
Um triângulo tem três medianas. Na figura, as três medianas são:
- AM1, mediana relativa ao lado BC ou ao vértice A;
- BM2, mediana relativa ao lado AC ou ao vértice B;
- CM3, mediana relativa ao lado AB ou ao vértice C.
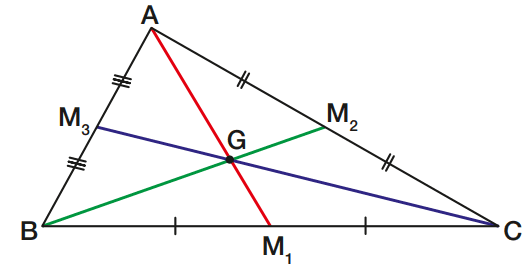
As três medianas de um triângulo encontram-se num ponto chamado baricentro do triângulo.
Na figura acima, G é o baricentro do triângulo ABC.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Leia também…
Pontos Notáveis do Triângulo e Propriedades
Lista de exercício com solução de Pontos Notáveis do Triângulo













