Multiplicação de Matrizes
A multiplicação de matrizes é uma das operações mais importantes da Álgebra Linear. Esse conteúdo é fundamental para provas do ENEM, vestibulares e concursos públicos. Se você está montando um cronograma de estudos, confira também os mapas mentais e o banco de questões.
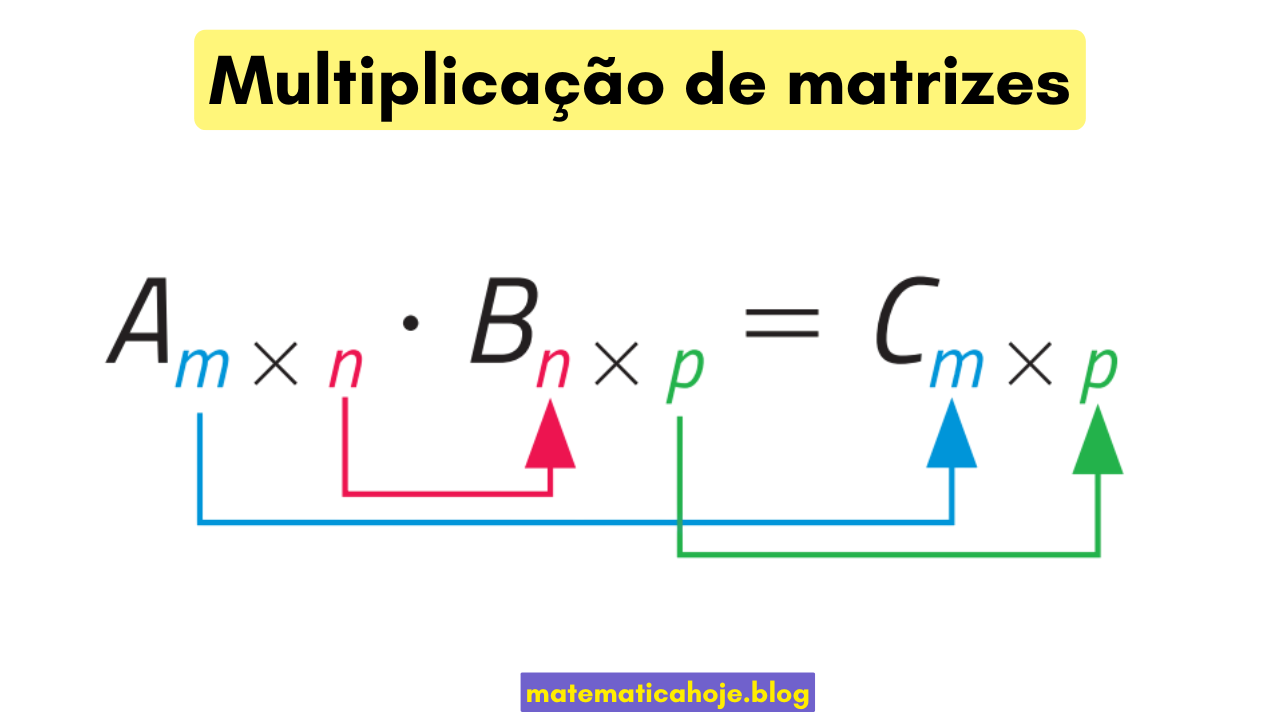
Definição
Seja \(A_{m\times n}\) uma matriz de ordem \(m\times n\) e \(B_{n\times p}\) uma matriz de ordem \(n\times p\). O produto \(A\cdot B\) será definido e resultará em uma matriz \(C_{m\times p}\).
Ou seja, cada elemento \(c_{ij}\) da matriz resultante é obtido pelo produto escalar entre a linha \(i\) de \(A\) e a coluna \(j\) de \(B\).
Exemplo passo a passo
Considere:
\( A=\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix}, \quad B=\begin{bmatrix}5 & 6\\7 & 8\end{bmatrix}. \)
O produto \(C=A\cdot B\) será uma matriz \(2\times 2\). Calculando cada elemento:
- \(c_{11}=1\cdot5+2\cdot7=5+14=19\)
- \(c_{12}=1\cdot6+2\cdot8=6+16=22\)
- \(c_{21}=3\cdot5+4\cdot7=15+28=43\)
- \(c_{22}=3\cdot6+4\cdot8=18+32=50\)
Logo, \( C=\begin{bmatrix}19 & 22\\43 & 50\end{bmatrix}. \)
Exercícios Resolvidos
Exercício 1: Calcule \(A\cdot B\), sendo
\( A=\begin{bmatrix}2 & 0\\1 & -1\end{bmatrix}, \quad B=\begin{bmatrix}3 & 4\\5 & 6\end{bmatrix}. \)
Mostrar solução
\( C=A\cdot B=\begin{bmatrix} 2\cdot3+0\cdot5 & 2\cdot4+0\cdot6\\ 1\cdot3+(-1)\cdot5 & 1\cdot4+(-1)\cdot6 \end{bmatrix} =\begin{bmatrix}6 & 8\\-2 & -2\end{bmatrix}. \)
Exercício 2: Calcule \(A\cdot B\), sendo
\( A=\begin{bmatrix}1 & 2 & 3\\0 & -1 & 4\end{bmatrix}, \quad B=\begin{bmatrix}2 & 1\\-3 & 0\\5 & -2\end{bmatrix}. \)
Mostrar solução
\( C=A\cdot B=\begin{bmatrix}
1\cdot2+2(-3)+3\cdot5 & 1\cdot1+2\cdot0+3(-2)\\
0\cdot2+(-1)(-3)+4\cdot5 & 0\cdot1+(-1)\cdot0+4(-2)
\end{bmatrix} \)
\(=\begin{bmatrix}2-6+15 & 1+0-6\\0+3+20 & 0+0-8\end{bmatrix}
=\begin{bmatrix}11 & -5\\23 & -8\end{bmatrix}. \)
Propriedades Importantes
- A multiplicação de matrizes não é comutativa: em geral, \(A\cdot B \neq B\cdot A\).
- É associativa: \((A\cdot B)\cdot C=A\cdot(B\cdot C)\).
- É distributiva em relação à adição: \(A(B+C)=AB+AC\).
- Existe uma matriz especial, a Matriz Identidade, que funciona como “elemento neutro” da multiplicação.
Continue estudando
Veja também nossos materiais complementares:





















