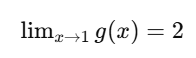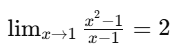Você já se perguntou o que acontece com uma função quando nos aproximamos de um ponto específico em seu domínio, mesmo que ela não esteja definida exatamente nesse ponto? Esse é o ponto de partida para o estudo de limites, um conceito fundamental no Cálculo Diferencial.
Neste artigo, vamos abordar a noção intuitiva de limites, explicando de forma simples como entender o comportamento de uma função nos arredores de um ponto, usando tabelas de aproximações e exemplos visuais. Se você está começando a estudar cálculo, este é o melhor lugar para começar!
O que é Limite? (Intuitivamente falando)
Em termos simples, o limite de uma função em um ponto representa o valor que a função tende a assumir conforme a variável independente (geralmente o x) se aproxima de um determinado valor.
Mesmo que a função não esteja definida exatamente nesse ponto, ainda assim podemos investigar seu comportamento próximo a ele. Isso nos dá uma poderosa ferramenta para estudar funções que apresentam “falhas” ou interrupções.
Compreensão Visual do Limite
Imagine o gráfico de uma função qualquer. Escolha um ponto específico no eixo x, digamos x = 1. Agora observe o que acontece com os valores de f(x) quando x se aproxima de 1 pela esquerda (valores menores) e pela direita (valores maiores).
Se os valores de f(x) se aproximam de um número específico L à medida que nos aproximamos de x = 1 por ambos os lados, dizemos que o limite de f(x) quando x tende a 1 é igual a L.
📌 Exemplo com gráfico:
(Sugestão de inserção manual: Gráfico de uma função com “buraco” no ponto x = 1, mas com valores se aproximando de L = 2 dos dois lados.)
Tabelas de Aproximações: Pela Esquerda e Pela Direita
Uma forma simples e prática de entender o comportamento de uma função ao redor de um ponto é usar tabelas de aproximações. Elas ajudam a visualizar como os valores de f(x) se comportam quando nos aproximamos de x por valores menores e maiores.
🔸 Aproximação pela esquerda (valores menores que 1):
| x | 0,9 | 0,99 | 0,999 |
|---|---|---|---|
| g(x) | 1,9 | 1,99 | 1,999 |
🔹 Aproximação pela direita (valores maiores que 1):
| x | 1,1 | 1,01 | 1,001 |
|---|---|---|---|
| g(x) | 2,1 | 2,01 | 2,001 |
Observe que conforme x se aproxima de 1, os valores de g(x) se aproximam de 2. Podemos escrever:
Mesmo que a função g(x) não esteja definida em x = 1!
Exemplo Prático: Limite com Indeterminação
Considere a função:
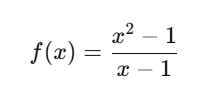
Se substituirmos x = 1, temos:
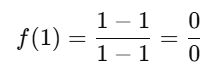
Isso é uma indeterminação. Mas veja o que acontece com os valores de f(x) próximos de 1:
| x | 0,9 | 0,99 | 1,01 | 1,1 |
|---|---|---|---|---|
| f(x) | 1,9 | 1,99 | 2,01 | 2,1 |
Com uma rápida fatoração:
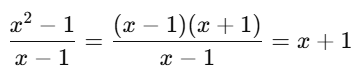
Logo:
Mesmo que a função original seja indefinida em x = 1, o limite existe e é igual a 2.
Por Que Essa Noção é Importante?
A ideia de limite está por trás de derivadas, integrais, assíntotas e continuidade. Mesmo quando a função “falha” em um ponto, o limite nos permite estudar seu comportamento de forma precisa e previsível.
Conclusão
A noção intuitiva de limites é a base para o entendimento de todo o cálculo. Ela permite que compreendamos como uma função se comporta nos arredores de um ponto, mesmo que esse ponto não esteja definido.
Utilizar gráficos e tabelas de aproximação é uma excelente maneira de ganhar familiaridade com o conceito. À medida que você se sentir mais confortável, poderá avançar para as definições formais e técnicas mais avançadas.
📚 Quer continuar aprendendo?
Nos próximos artigos, exploraremos:
- Limites laterais e limites infinitos
- Limites no infinito
- Continuidade de funções
- Tipos de descontinuidade
Fique de olho no blog e compartilhe este artigo com quem também está estudando cálculo!
