Questão 7 – OBMEP 2024
Felipe vai colorir a figura de modo que regiões vizinhas tenham cores diferentes. Qual é o menor número de cores que ele deve usar?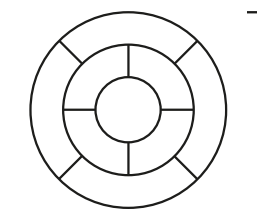
Alternativas:
- (A) 4
- (B) 2
- (C) 3
- (D) 6
- (E) 5
Ver Solução
Entendendo o enunciado:
A figura é formada por três camadas: uma região central, uma camada intermediária com 4 regiões, e uma camada externa também com 4 regiões. O objetivo é pintar essas regiões de forma que nenhuma região vizinha compartilhe a mesma cor.
Análise:
Podemos decompor a figura:
- 1 cor para a região central.
- Na camada intermediária, precisamos de 2 cores diferentes da central para pintar regiões opostas sem repetir.
- Na camada externa, também usamos 2 cores diferentes da intermediária, mas uma delas pode coincidir com a da região central.
Somando:
\( 1 \text{ (central)} + 2 \text{ (intermediária)} + 1 \text{ (externa)} = 4 \) cores no total.
Prova por impossibilidade:
Suponha que fosse possível usar apenas 3 cores (A, B e C). Como algumas regiões têm até 5 vizinhos, será impossível pintar sem repetir cores em pelo menos uma região, como mostrado nos diagramas do gabarito oficial.
Conclusão:
O menor número de cores que Felipe pode usar para pintar a figura corretamente é 4 cores.
Gabarito: Letra A
🧠 Mapas Mentais de Matemática





















