Área na malha triangular – Decomposição e contagem
Questão 4 – OBMEP 2024 – Nível 2
A figura apresenta uma malha triangular formada por triângulos equiláteros pequenos, cada um com área igual a 1 cm². Qual é a área, em centímetros quadrados, da região cinza?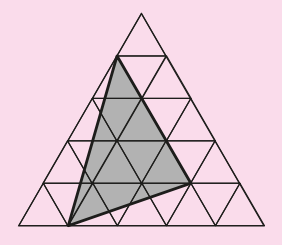
Alternativas:
- (A) 11
- (B) 7
- (C) 10
- (D) 8
- (E) 9
Ver Solução
Entendendo o enunciado: A figura mostra uma malha de triângulos equiláteros. Cada triângulo pequeno tem área igual a 1 cm². A região cinza é composta por triângulos completos e metades de triângulos pequenos.
Dividindo a região cinza conforme indicado na imagem da solução, obtemos dois triângulos sobrepostos equivalentes a um único triângulo maior destacado na Figura 3.
Esse triângulo destacado possui base com 3 triângulos pequenos e altura com 3 camadas de triângulos. Assim, ele é formado por exatamente:
9 triângulos pequenos
Logo, a área da região cinza também é:
Área = 9 cm²
Outra forma de resolver: Como indicado no diagrama com setas, temos:
- Uma região com metade de 6 triângulos → 3
- Uma região com metade de 4 triângulos → 2
- Uma região com 4 triângulos inteiros → 4
Total: \(3 + 2 + 4 = 9\) cm²
Gabarito: Letra E
🧠 Mapas Mentais de Matemática
























