OBMEP 2024 – Nível 3 – Questão 12
Enunciado:
Considere um hexágono regular de área 1 e todos os triângulos cujos vértices são também vértices do hexágono. Qual é a soma das áreas de todos esses triângulos?
(A) 6
(B) 7
(C) 5
(D) 4
(E) 3
Ver Solução
Entendendo o enunciado: Queremos somar as áreas de todos os triângulos possíveis formados apenas com os vértices do hexágono regular de área 1.
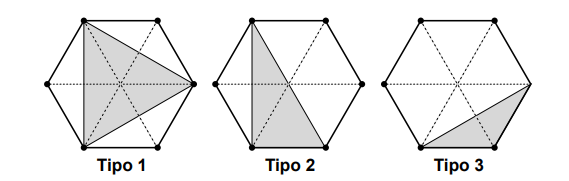
Classificamos os triângulos em três tipos:
- Tipo 1: Triângulos cujos vértices não são consecutivos no hexágono.
Exemplos: ACE e BDF. - Tipo 2: Triângulos com dois vértices consecutivos e o terceiro separado.
Exemplos: ABD, ABE, BCE, BCF, CDF, CDA, DEA, DEB, EFB, EFC, FAC, FAD. - Tipo 3: Triângulos com três vértices consecutivos no hexágono (triângulos formados diretamente por três lados adjacentes).
Exemplos: ABC, BCD, CDE, DEF, EFA, FAB.
Quantidades:
- 2 triângulos do Tipo 1
- 12 triângulos do Tipo 2
- 6 triângulos do Tipo 3
Áreas relativas:
- Cada triângulo do Tipo 1 tem área igual a \( \frac{1}{2} \) da área do hexágono.
- Cada triângulo do Tipo 2 tem área igual a \( \frac{1}{3} \) da área do hexágono.
- Cada triângulo do Tipo 3 tem área igual a \( \frac{1}{6} \) da área do hexágono.
Calculando a soma total das áreas:
\( 2 \times \frac{1}{2} + 12 \times \frac{1}{3} + 6 \times \frac{1}{6} = \)
\( 1 + 4 + 1 = \) 6
Resposta correta: (A) 6