Enunciado:
Pedro colocou os números 1, 2, 3, 4 e 5 nas casas do tabuleiro abaixo, um número em cada casa, sem repetir números nas linhas e nas colunas. Em seguida, ele somou os oito números colocados na primeira e na última colunas. Qual dos números abaixo não pode ser um resultado para a soma que Pedro fez?
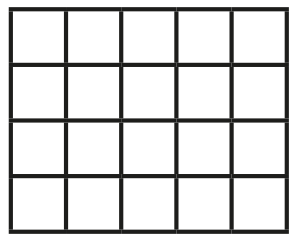
- (A) 20
- (B) 23
- (C) 26
- (D) 25
- (E) 21
Ver Solução
Um preenchimento válido usa os números 1 a 5, uma vez em cada linha e coluna (sem repetição). A pergunta pede a soma dos números das colunas extremas (1ª e 5ª colunas).
Para encontrar o menor valor possível, use apenas números de 1 a 4 nas colunas extremas:
| 1 | 2 | |||
| 2 | 1 | |||
| 3 | 4 | |||
| 4 | 3 |
Soma: \(1+2+3+4+2+1+4+3 = 20\)
Mas ao tentar usar o número 5 no restante do tabuleiro, ele precisa aparecer 4 vezes em 3 colunas restantes — isso levaria à repetição, o que é inválido.
Portanto, não é possível ter soma igual a 20.
Agora veja um arranjo válido geral, com estrutura:
| a | c | d | e | b |
| b | d | e | c | a |
| c | e | b | a | d |
| d | a | c | b | e |
| e | b | a | d | c |
Com a escolha de valores distintos para a, b, c, d, e, temos:
| a | b | c | d | e | Soma das colunas extremas |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 21 |
| 1 | 3 | 4 | 5 | 2 | 22 |
| 1 | 4 | 5 | 2 | 3 | 23 |
| 1 | 5 | 2 | 3 | 4 | 24 |
| 2 | 3 | 4 | 5 | 1 | 25 |
| 2 | 4 | 5 | 1 | 3 | 26 |
| 2 | 5 | 1 | 3 | 4 | 27 |
Portanto, todas as somas de 21 a 27 são possíveis, mas 20 não é possível.
Resposta correta: Letra (A)
🧠 Mapas Mentais de Matemática





















