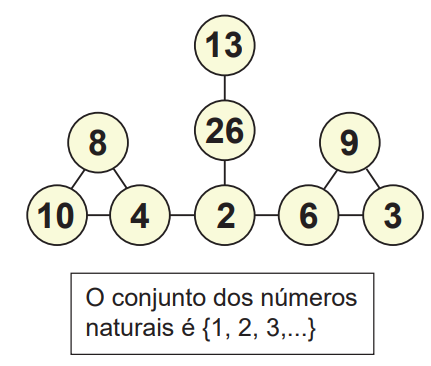
Questão 04. Os círculos do diagrama devem ser preenchidos com números naturais diferentes. Dois números escritos em círculos ligados por um segmento devem ter um divisor comum maior que 1.
Por exemplo, 8 e 15 nunca vão se ver em círculos ligados por um segmento. Abaixo temos um exemplo de preenchimento:
a) Faça um preenchimento para os círculos vazios abaixo.
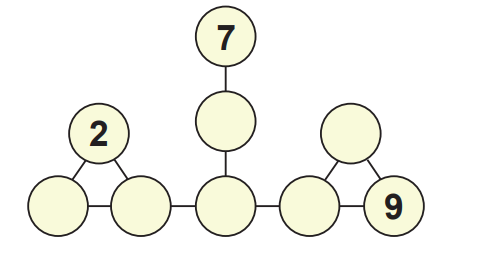
b) Preencha os círculos de modo que o maior número escrito seja 12.
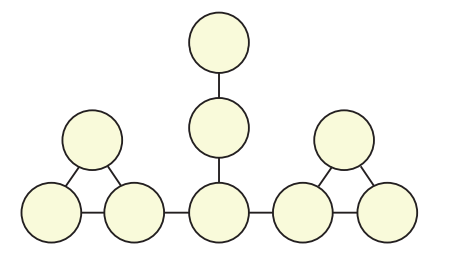
c) Explique por que é impossível preencher os círculos de modo que o maior número escrito seja menor do que 12.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Os números precisam ter divisores comuns (maior que 1) quando estão conectados, e todos devem ser distintos. O desafio é preencher respeitando essa condição e minimizando o maior número usado, especialmente no item c).
1) Item a) – Preenchimento possível:

Um exemplo válido é:
7, 10, 70, 21, 6, 9
Todos os pares conectados têm um divisor comum maior que 1. Por exemplo:
- 10 e 70 têm divisor comum 10
- 70 e 21 têm divisor comum 7
- 6 e 9 têm divisor comum 3
✅ Conclusão do item a):
- O preenchimento respeita todas as condições de divisibilidade.
2) Item b) – Preenchimento com maior número igual a 12:

Exemplo de preenchimento:
5, 3, 6, 12, 9, 4, 8
Todos os pares conectados têm divisores comuns maiores que 1, e o maior número utilizado é 12.
✅ Conclusão do item b):
- O preenchimento é possível com o maior número sendo exatamente 12.
3) Item c) – Por que não é possível preencher com números menores que 12:
Se o maior número for menor que 12, os números disponíveis se restringem a 1 até 11. No entanto:
- O número 1 nunca pode ser usado (não tem divisor comum com nenhum outro além de 1).
- Números primos pequenos, como 7 e 11, não são bons candidatos pois seus múltiplos estão acima de 11.
- Com 8 círculos a preencher e restrições de ligação, é impossível selecionar 8 números distintos todos com divisores comuns com seus vizinhos.
Portanto, abaixo de 12 não é possível montar um diagrama completo e válido.
✅ Conclusão do item c):
- Não há como preencher os círculos de forma válida com todos os números menores que 12.






















