Questão 05. Janaína tem vários dados idênticos com faces numeradas de 1 a 6. Nesses dados, a soma dos números em faces opostas é sempre igual a 7. Ela cola alguns desses dados e coloca adesivos nas faces não coladas, inclusive nas faces que estão em contato com a mesa.
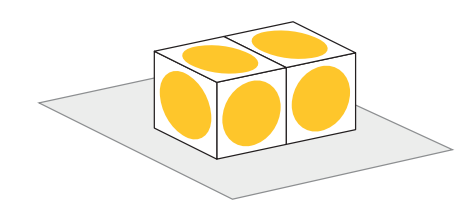
a) Qual é a menor soma possível para todos os números que foram cobertos por adesivos nos dois dados colados abaixo?
b) Janaína colou vários dados como mostrado abaixo. Quantos adesivos ela usou?
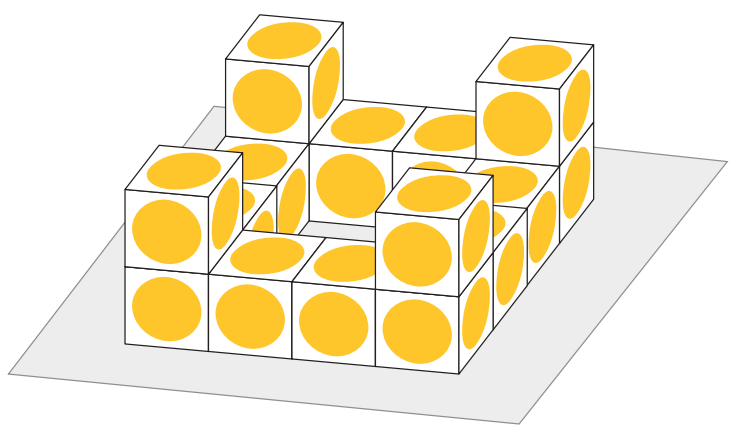
c) Na colagem de dados do item b), qual é a menor soma possível para todos os números que foram cobertos por adesivos?
🔍 Ver solução passo a passo
1) Item a – Menor soma possível dos números cobertos nos dois dados colados:
As faces de um dado somam: $$1 + 2 + 3 + 4 + 5 + 6 = 21$$
Em dois dados: $$2 \times 21 = 42$$
A menor soma possível para as faces cobertas por adesivos ocorre quando as faces coladas entre os dados são aquelas com os maiores números, ou seja, os números 6. Isso deixa os menores valores disponíveis para os adesivos.
Se duas faces coladas somam $$6 + 6 = 12$$, então os adesivos cobrem: $$42 – 12 = 30$$
✅ Conclusão do item a):
- Menor soma possível para os números cobertos por adesivos: $$30$$
2) Item b – Quantos adesivos foram usados?
Há 16 dados no total.
- 4 dados no topo → $$4 \times 5 = 20$$ faces adesivadas
- 4 dados abaixo do topo → $$4 \times 3 = 12$$ faces adesivadas
- 8 dados na base → $$8 \times 4 = 32$$ faces adesivadas
Total de adesivos:
$$20 + 12 + 32 = 64$$
✅ Conclusão do item b):
- Quantidade total de adesivos usados: $$64$$
3) Item c – Menor soma possível para os números cobertos por adesivos (caso b):
A menor soma ocorre quando as faces coladas são aquelas com os maiores valores, de forma que os adesivos cubram os menores.
- Faces adesivadas dos 4 dados do topo: $$4 \times (1 + 2 + 3 + 4 + 5) = 4 \times 15 = 60$$
- Faces adesivadas dos 4 dados abaixo: $$4 \times (1 + 2 + 3) = 12$$
- Faces adesivadas dos 8 dados na base: $$8 \times 7 = 56$$
Total:
$$60 + 12 + 56 = 128$$
✅ Conclusão do item c):
- Menor soma possível dos números cobertos por adesivos: $$128$$






















