Enunciado:
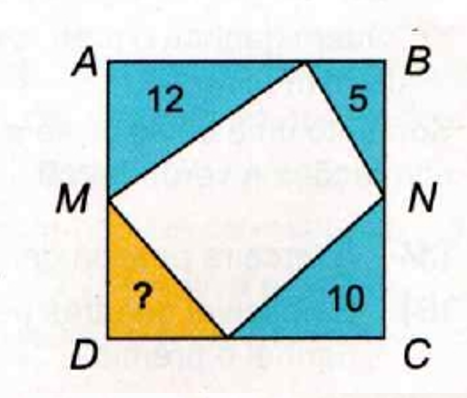
Na figura, \(ABCD\) é um retângulo. Os pontos \(M\) e \(N\) são pontos médios dos lados \(AD\) e \(BC\). As áreas dos triângulos azuis são 12, 5 e 10. Qual é a área do triângulo amarelo?
Alternativas:
- (A) 7
- (B) 6
- (C) 8
- (D) 5
- (E) 9
Ver Solução
1. Entendendo a figura:
O retângulo foi dividido em quatro triângulos por diagonais que ligam os pontos médios dos lados opostos.
Os triângulos azuis têm áreas: 12 (superior esquerdo), 5 (superior direito) e 10 (inferior direito).
2. Raciocínio por simetria:
Como \(M\) e \(N\) são pontos médios, os segmentos traçados formam regiões com propriedades simétricas e áreas proporcionais.
Os triângulos \(PMN\) (superior) e \(QNM\) (inferior) têm a mesma altura relativa e mesma base (já que \(MN\) é comum).
Logo, as áreas dos triângulos inferiores são proporcionais às áreas superiores opostas.
3. Cálculo:
A área total do quadrilátero interno é a soma das quatro áreas triangulares:
\[ 12 + 5 + 10 + ? = \text{total} \Rightarrow ? = \text{área restante} = 7 \]
✅ Gabarito: Letra A
🧠 Mapas Mentais de Matemática
























