Enunciado:
Em um tabuleiro \(6 \times k\), podemos colocar uma peça \(2 \times 3\) na vertical ou horizontal de 76 maneiras distintas. Qual é o valor de \(k\)?
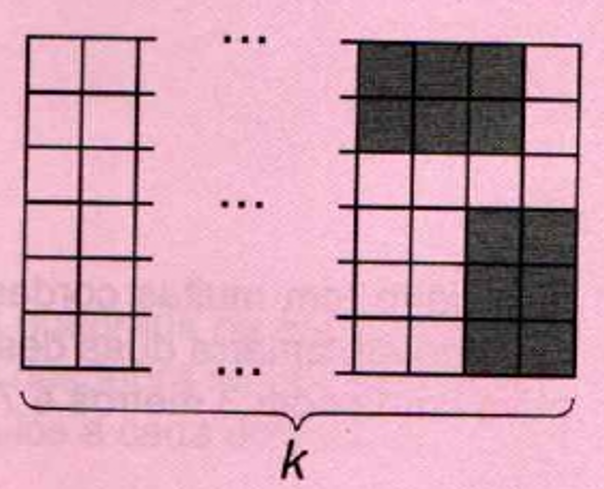
Alternativas:
- (A) 10
- (B) 12
- (C) 14
- (D) 20
- (E) 7
Ver Solução
1. Conceito:
Uma peça \(2 \times 3\) pode ser colocada deitada (horizontal) ou em pé (vertical). O tabuleiro tem 6 linhas e \(k\) colunas.
2. Casos possíveis:
- Para colocar deitada (\(2 \times 3\)): precisa de 2 linhas e 3 colunas.
Podemos escolher 5 linhas (6 − 1) e \(k − 2\) colunas para a posição inicial.
Total: \(5 \times (k – 2)\) - Para colocar em pé (\(3 \times 2\)): precisa de 3 linhas e 2 colunas.
Podemos escolher 4 linhas (6 − 2) e \(k − 1\) colunas.
Total: \(4 \times (k – 1)\)
3. Soma total:
\[ 5(k – 2) + 4(k – 1) = 76 \]
\[ 5k – 10 + 4k – 4 = 76 \]\[\Rightarrow 9k – 14 = 76\]\[\ \Rightarrow 9k = 90 \Rightarrow \boxed{k = 10} \]
✅ Gabarito: Letra A
🧠 Mapas Mentais de Matemática












