Enunciado:
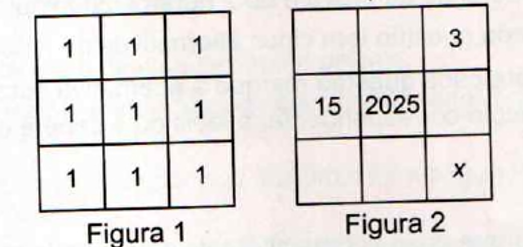
Maria coloca inicialmente o número 1 nos nove quadradinhos de um quadriculado 3×3 (Figura 1). Depois, ela escolhe quatro quadradinhos com um mesmo vértice comum e multiplica os quatro números desses quadradinhos por um mesmo valor. Após fazer isso algumas vezes, os números no quadriculado ficaram como na Figura 2.
Qual é o valor de x?
Alternativas:
- (A) 75
- (B) 9
- (C) 135
- (D) 25
- (E) 45
Ver Solução
1. Estratégia:
Como cada multiplicação envolve 4 quadrados conectados por um mesmo vértice, toda vez que aplicamos um fator em um desses “subtabuleiros”, ele afeta o valor da casa central (meio da matriz).
2. Observação:
A casa do meio (onde está o número 2025) pertence a 4 subtabuleiros (um para cada vértice do 3×3). Ou seja, ela foi multiplicada por 4 fatores diferentes.
Os subtabuleiros responsáveis pelos valores:
- O subtabuleiro superior direito tem o número 3
- O subtabuleiro do lado esquerdo tem o número 15
- O inferior direito tem o número x
- Há um quarto valor desconhecido, mas não afeta nossa conta, pois vamos usar 2025 diretamente.
3. Fatoração:
Como 2025 = 3 × 15 × x, podemos calcular:
\[ x = \frac{2025}{3 \times 15} = \frac{2025}{45} = \boxed{45} \]
✅ Gabarito: Letra E
🧠 Mapas Mentais de Matemática












