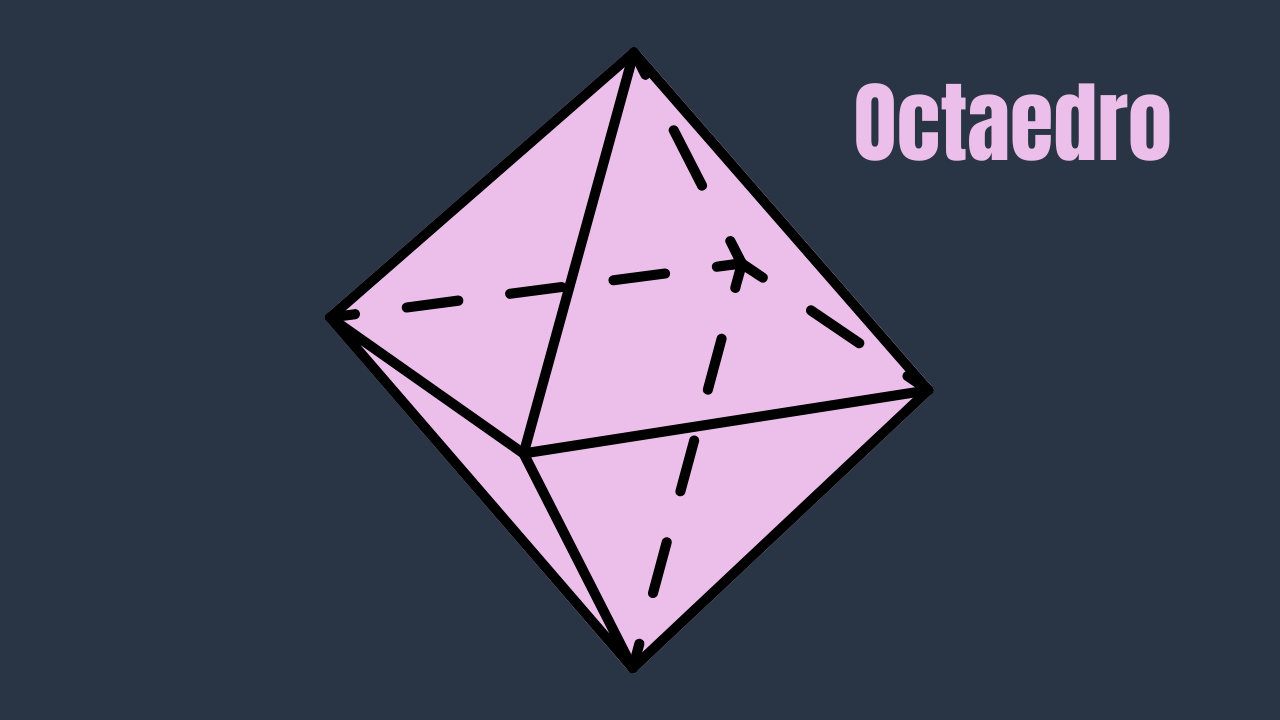
Octaedro – definição, propriedades, fórmulas e exercícios
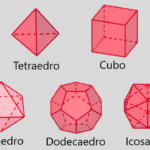
O octaedro regular é um dos Sólidos de Platão. Possui oito faces congruentes em forma de triângulos equiláteros, 12 arestas e 6 vértices. É o dual do cubo (hexaedro regular): os vértices do octaedro correspondem aos centros das faces do cubo e vice-versa.
- a — comprimento da aresta (lado dos triângulos);
- A_t — área total; V — volume;
- R — raio da esfera circunscrita (passa pelos vértices);
- r — raio da esfera inscrita (tangente às faces);
- ρ — raio até o centro das arestas (esfera “média”).
Propriedades e fórmulas básicas
| Grandeza | Fórmula (em função de \(a\)) | Observação |
|---|---|---|
| Número de faces (F) | 8 | Triângulos equiláteros |
| Nº de arestas (A) | 12 | — |
| Nº de vértices (Vértices) | 6 | — |
| Área total \(A_t\) | \(A_t=2\sqrt{3}\,a^2\) | 8 faces × \(\frac{\sqrt{3}}{4}a^2\) |
| Volume \(V\) | \(V=\dfrac{\sqrt{2}}{3}\,a^3\) | ver decomposição abaixo |
| Raio circunscrito \(R\) | \(R=\dfrac{a}{\sqrt{2}}\) | distância do centro a um vértice |
| Raio inscrito \(r\) | \(r=\dfrac{a}{\sqrt{6}}=\dfrac{\sqrt{6}}{6}a\) | distância do centro a uma face |
| Raio até arestas \(ρ\) | \(ρ=\dfrac{a}{2}\) | distância do centro ao meio de uma aresta |
Característica de Euler (checagem): \(V – A + F = 6 – 12 + 8 = 2\).
Ângulo diedro interno: \(\cos\delta=-\tfrac{1}{3}\Rightarrow \delta\approx 109{,}47^\circ\).
Decomposição em duas pirâmides quadrangulares
Um octaedro regular pode ser visto como duas pirâmides de base quadrada coladas pela base. O “quadrado equatorial” tem lado \(a\) e a altura de cada pirâmide é \(h=\dfrac{a}{\sqrt{2}}\). Assim:
Volume de uma pirâmide: \(V_1=\dfrac{1}{3}\,a^2\cdot\dfrac{a}{\sqrt{2}}=\dfrac{a^3}{3\sqrt{2}}\).
Volume do octaedro: \(V=2V_1=\dfrac{\sqrt{2}}{3}\,a^3\).
Por dualidade, muitas contas do cubo/hexaedro ajudam a deduzir relações para o octaedro.
Exemplo resolvido
Exemplo. Um octaedro tem aresta \(a=6\ \text{cm}\). Calcule \(A_t\), \(V\) e os raios \(R\) e \(r\).
\(A_t=2\sqrt{3}\cdot 36=72\sqrt{3}\ \text{cm}^2\).
\(V=\dfrac{\sqrt{2}}{3}\cdot 216=72\sqrt{2}\ \text{cm}^3\).
\(R=\dfrac{a}{\sqrt{2}}=3\sqrt{2}\ \text{cm}\), \(\quad r=\dfrac{a}{\sqrt{6}}=\dfrac{6}{\sqrt{6}}=\sqrt{6}\ \text{cm}\).
Exercício Octaedro: 10 Situações-Problema
Quando precisar, use \( \sqrt{2}\approx1{,}414 \) e \( \sqrt{3}\approx1{,}732 \).
Q1 — Pintura de um enfeite geométrico
Um pingente em formato de octaedro tem aresta \(a=5\text{ cm}\). O verniz custa R$ 0,12 por cm². Qual será o custo para envernizar todas as faces?
Área total \(A_t=2\sqrt{3}\,a^2=2\sqrt{3}\cdot25=50\sqrt{3}\approx86{,}60\ \text{cm}^2\).
Custo \(\approx0{,}12\times86{,}60=\mathbf{R\$\,10{,}39}\).
Q2 — Impressão 3D por volume
Um protótipo de octaedro com aresta \(a=8\text{ cm}\) será impresso em resina que custa R$ 0,05 por cm³. Quanto será gasto?
\(V=\dfrac{\sqrt{2}}{3}a^3=\dfrac{\sqrt{2}}{3}\cdot512=\dfrac{512\sqrt{2}}{3}\approx241{,}42\ \text{cm}^3\).
Custo \(\approx0{,}05\times241{,}42=\mathbf{R\$\,12{,}07}\).
Q3 — Projeto com área especificada
Um designer quer um octaedro cuja área total seja \(200\sqrt{3}\ \text{cm}^2\). Determine a aresta e o volume.
\(2\sqrt{3}\,a^2=200\sqrt{3}\Rightarrow a^2=100\Rightarrow a=\mathbf{10\text{ cm}}\).
\(V=\dfrac{\sqrt{2}}{3}\cdot10^3=\dfrac{1000\sqrt{2}}{3}\approx\mathbf{471{,}41\ \text{cm}^3}\).
Q4 — Peça dentro de uma “bolha” esférica
Uma escultura em octaedro será embalada numa esfera inflável de raio \(R=6\sqrt{2}\ \text{cm}\) (esfera circunscrita). Qual é a aresta e o volume da escultura?
No octaedro, \(R=\dfrac{a}{\sqrt{2}}\Rightarrow a=R\sqrt{2}=12\ \text{cm}\).
\(V=\dfrac{\sqrt{2}}{3}\cdot12^3=576\sqrt{2}\approx\mathbf{814{,}59\ \text{cm}^3}\).
Q5 — Móbile com esfera inscrita
Um móbile contém um octaedro que envolve exatamente uma esfera de raio \(r=3\ \text{cm}\) (esfera inscrita). Calcule a aresta e a área total.
\(r=\dfrac{a}{\sqrt{6}}\Rightarrow a=3\sqrt{6}\approx7{,}35\ \text{cm}\).
\(a^2=54\Rightarrow A_t=2\sqrt{3}\cdot54=\mathbf{108\sqrt{3}\approx187{,}06\ \text{cm}^2}\).
Q6 — Estrutura de arestas metálicas
Para montar a armação de um octaedro com barras de \(a=0{,}40\ \text{m}\) (uma por aresta), quanto de material comprar, considerando 10% de sobra?
São 12 arestas. Comprimento útil \(=12\cdot0{,}40=4{,}8\ \text{m}\).
Com 10% de sobra: \(4{,}8\times1{,}10=\mathbf{5{,}28\ \text{m}}\).
Q7 — Maquete em escala
Um modelo tem aresta \(4\ \text{cm}\). A peça real será \(2{,}5\) vezes maior em cada dimensão. Calcule a área total real e o volume real.
Aresta real: \(a_r=10\ \text{cm}\).
\(A_{t,r}=2\sqrt{3}\cdot10^2=\mathbf{200\sqrt{3}\approx346{,}41\ \text{cm}^2}\).
\(V_r=\dfrac{\sqrt{2}}{3}\cdot10^3=\mathbf{\dfrac{1000\sqrt{2}}{3}\approx471{,}41\ \text{cm}^3}\).
Q8 — Tamanho máximo ponta a ponta
Um octaedro de aresta \(a=9\ \text{cm}\) deve caber numa embalagem bolha. Qual é o diâmetro mínimo da bolha para conter o sólido de ponta a ponta?
O diâmetro é \(2R\) e \(R=\dfrac{a}{\sqrt{2}}\Rightarrow 2R=a\sqrt{2}\).
\(d=\sqrt{2}\cdot9\approx\mathbf{12{,}73\ \text{cm}}\).
Q9 — Crescimento dimensional
Um octaedro tem aresta \(a\). Ele é redesenhado com aresta \(1{,}10\,a\) (aumento de 10%). Em que fatores crescem a área total e o volume?
Áreas escalam com \(k^2\): \(1{,}10^2=\mathbf{1{,}21}\). Volumes escalam com \(k^3\): \(1{,}10^3=\mathbf{1{,}331}\).
Q10 — Derretimento de um octaedro de gelo
Um octaedro de gelo tem aresta \(12\ \text{cm}\) e perde 30% do volume por derretimento. Qual passa a ser a nova aresta?
Volume novo \(=0{,}70\,V\). Como \(V\propto a^3\), \(a_{\text{novo}}=a\,(0{,}70)^{1/3}\approx 12\times0{,}8879=\mathbf{10{,}66\ \text{cm}}\).
Continue estudando
- Sólidos de Platão (octaedro, cubo, tetraedro, dodecaedro e icosaedro).
- Dualidade com o hexaedro (cubo).
- Fundamentos de pirâmides e pirâmide regular (decomposição do octaedro em pirâmides).