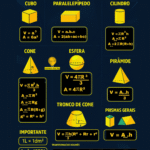
Paralelepípedo e Cubo — Volume e Área Total (com Exercícios Resolvidos)
Guia rápido e completo para calcular volume e área total do paralelepípedo e do cubo. Inclui exemplos passo a passo e lista de exercícios.

O que são Paralelepípedo e Cubo?
Paralelepípedo é um prisma cujas faces são paralelogramos. No caso mais comum (reto e retângulo), todas as faces são retângulos, com arestas medindo a, b e c.
Cubo é um caso particular de paralelepípedo retângulo em que a = b = c; todas as faces são quadrados congruentes.
Fórmulas Essenciais
Paralelepípedo (a, b, c)
Volume: \( V = a \cdot b \cdot c \)
Área Total: \( A_T = 2(ab + ac + bc) \)
Extras úteis: diagonal do sólido \( d = \sqrt{a^2 + b^2 + c^2} \).
Cubo (aresta a)
Volume: \( V = a^3 \)
Área Total: \( A_T = 6a^2 \)
Extras: diagonal da face \( d_f = a\sqrt{2} \) e diagonal do cubo \( d = a\sqrt{3} \).
Revise estes tópicos com os Mapas Mentais de Matemática e veja questões no Banco de Questões.
Exemplos Resolvidos
Exemplo 1 — Volume do Paralelepípedo
Enunciado. Em um paralelepípedo retângulo, \( a=6 \) cm, \( b=4 \) cm e \( c=10 \) cm. Calcule o volume.
Ver solução
\( V = a \cdot b \cdot c \)
\( V = 6 \cdot 4 \cdot 10 \)
\( V = 24 \cdot 10 \)
\( V = \mathbf{240\ \text{cm}^3} \)
Exemplo 2 — Área Total do Cubo
Enunciado. Um cubo de aresta \( a=7 \) cm. Determine a área total.
Ver solução
\( A_T = 6a^2 \)
\( A_T = 6 \cdot 7^2 \)
\( A_T = 6 \cdot 49 \)
\( A_T = \mathbf{294\ \text{cm}^2} \)
📘 eBook Grátis — Fórmulas Matemática
Todas as fórmulas em um só lugar para revisar antes das provas e concursos.
➡️ Baixar AgoraExercícios Propostos
Resolva e depois confira o gabarito em cada questão. Quer mais? Veja o Banco de Questões e os 10 eBooks.
1) Calcule o volume de um paralelepípedo com \( a=5 \) cm, \( b=3 \) cm e \( c=14 \) cm.
Ver solução
\( V = 5\cdot3\cdot14 \)
\( V = 15\cdot14 \)
\( V = \mathbf{210\ \text{cm}^3} \)
2) (Múltipla escolha) Um paralelepípedo tem \( a=8 \) cm, \( b=2 \) cm e \( c=5 \) cm. O volume é:
- 70 cm³
- 80 cm³
- 90 cm³
- 100 cm³
Ver solução
3) Para \( a=4 \) cm, \( b=6 \) cm e \( c=9 \) cm, determine \( A_T \) do paralelepípedo.
Ver solução
\( A_T=2(4\cdot6+4\cdot9+6\cdot9) \)
\( A_T=2(24+36+54) \)
\( A_T=2\cdot114 \)
\( A_T=\mathbf{228\ \text{cm}^2} \)
4) Um cubo tem volume \( 343\ \text{cm}^3 \). Calcule a aresta.
Ver solução
5) (Múltipla escolha) Se o cubo tem \( a=3 \) cm, então \( A_T \) é:
- 36 cm²
- 48 cm²
- 54 cm²
- 72 cm²
Ver solução
6) Em um paralelepípedo, \( a=10 \) cm e \( b=12 \) cm. Sabendo que \( d=\sqrt{a^2+b^2+c^2}=19 \) cm, determine \( c \).
Ver solução
\( 361=100+144+c^2 \)
\( c^2=361-244=117 \)
\( c=\sqrt{117}\approx \mathbf{10.82\ \text{cm}} \)
7) Um paralelepípedo tem \( A_T=352 \) cm² e dimensões \( a=8 \) cm, \( b=6 \) cm. Encontre \( c \).
Ver solução
\( 2(48+8c+6c)=352 \)
\( 2(48+14c)=352 \)
\( 96+28c=352 \)
\( 28c=256 \Rightarrow c=\mathbf{9.14\ \text{cm}} \) (aprox.)
8) Uma caixa de papelão (paralelepípedo) mede 30 cm × 20 cm × 12 cm. Quantos litros cabem? (1 L = 1000 cm³)
Ver solução
\( 7200/1000=\mathbf{7.2\ L} \)
9) Um cubo tem diagonal do sólido \( d=12\sqrt{3} \) cm. Determine \( a \) e \( A_T \).
Ver solução
\( A_T=6a^2=6\cdot144=\mathbf{864\ \text{cm}^2} \)
10) (Teoria) Assinale a alternativa falsa:
- Em cubos, todas as faces são quadrados congruentes.
- A diagonal do cubo é maior que a diagonal de uma face.
- O volume do paralelepípedo depende apenas do perímetro das faces.
- Para paralelepípedo, \( A_T = 2(ab+ac+bc) \).