Permutação Simples, Circular e com Repetição

Quando pensamos em organizar ou rearranjar objetos, estamos lidando com o conceito de permutação. Esse princípio fundamental da análise combinatória é amplamente usado para resolver problemas onde a ordem dos elementos importa. Desde organizar livros em uma prateleira até criar senhas, as permutações ajudam a calcular todas as possibilidades.

Neste artigo, vamos desvendar as permutações de forma simples e prática, abordando os dois tipos principais: permutação simples e permutação com elementos repetidos.

📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade

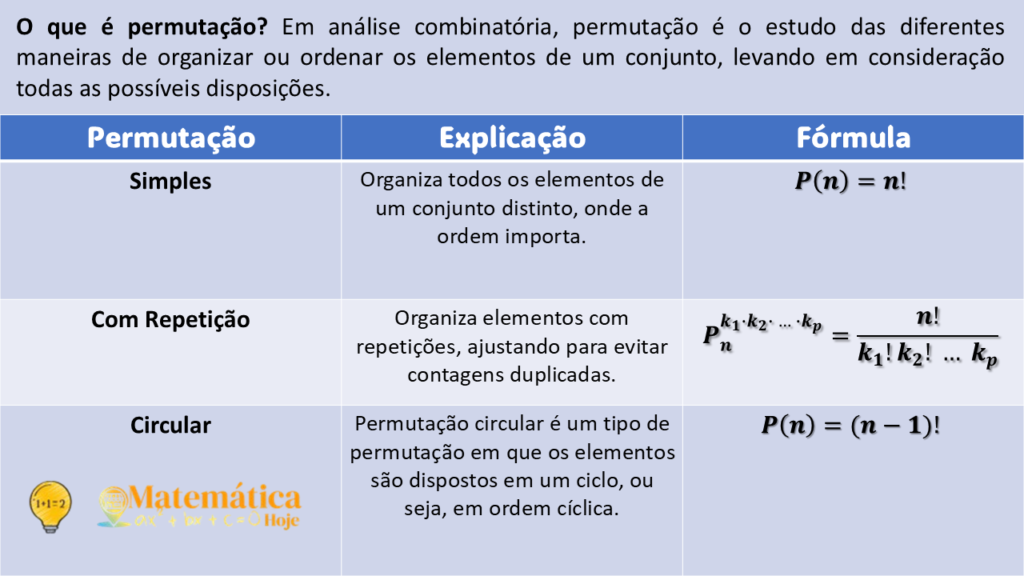
O Que é Permutação?

A permutação se refere ao número de maneiras pelas quais podemos organizar ou rearranjar elementos em diferentes ordens. Quando reorganizamos todos os elementos de um conjunto, estamos criando permutações.

Por exemplo:

• Ao organizar as letras A, B e C, podemos formar: ABC, ACB, BAC, BCA, CAB, CBA.
• Aqui, a ordem importa, pois ABC é diferente de CAB.

1. Permutação Simples

A permutação simples é utilizada quando todos os elementos de um conjunto são únicos, ou seja, não há repetição. O número de permutações é dado pelo fatorial (n!) do total de elementos (n).

Como Calcular?

A fórmula para permutação simples é: P(n) = n!

Onde n!n! (lê-se “n fatorial”) é o produto de todos os números inteiros positivos até nn.

Exemplo Prático:

Imagine que você tem 4 livros diferentes e deseja organizá-los em uma prateleira. Quantas maneiras diferentes existem para fazer isso?

• Total de elementos: n = 4.
• Cálculo:

P(4) = 4! = 4×3×2×1 = 24

Portanto, há 24 formas diferentes de organizar os 4 livros.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!

2. Permutação com Elementos Repetidos

Quando um conjunto possui elementos repetidos, reorganizá-los não cria combinações distintas. Nesse caso, usamos a fórmula de permutação com repetição para ajustar o número total de arranjos.

Como Calcular?

A fórmula é:

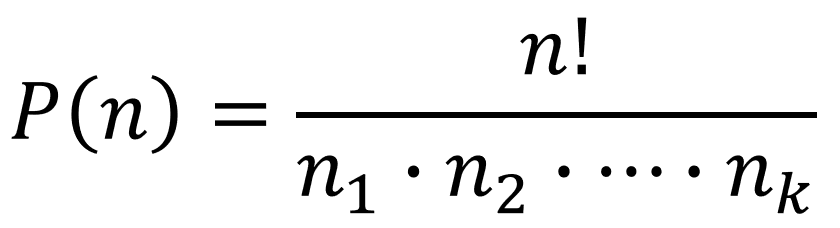
• n!: fatorial do número total de elementos.
• n₁, n₂, …,n_k!: fatoriais das repetições de cada elemento.

Exemplo Prático:

1 – Quantas palavras diferentes podem ser formadas com as letras da palavra “BOLA”?

• Total de letras: 4 (B, O, L, A).
• Não há repetição de letras.

Aqui, o número total de permutações será:

P(4) = 4! = 4×3×2×1 = 24

2 – Agora, considere a palavra “ANA”, onde a letra A se repete 2 vezes:

• Total de letras: 3 (A, N, A).
• A letra A se repete 2 vezes.

Cálculo:

P = 3!/2! = 6/2 = 3

As palavras formadas são: ANA, NAA, AAN.

3 – Quantas palavras diferentes podem ser formadas com as letras da palavra “BALA”?

• Total de letras: 4 (B, A, L, A).
• A letra A se repete 2 vezes.

Aqui, o número total de permutações será:

P(4) = 4!/2! = 4×3 = 12

“Quer dominar os cálculos de possibilidades e resolver problemas de contagem com facilidade? Confira nosso artigo completo sobre as Fórmulas da Análise Combinatória e aprenda como aplicá-las no seu dia a dia com exemplos claros e objetivos!

3. Permutação Circular

A permutação circular ocorre quando os elementos são dispostos em forma de círculo, como em uma mesa redonda. Nesse caso, a ordem importa, mas as posições relativas entre os elementos são o que realmente conta, pois girar o círculo não cria novas permutações.

Fórmula:

P_c = (n-1)!

• n: número total de elementos no círculo.

Exemplo:

Quantas maneiras diferentes 4 pessoas podem se sentar em uma mesa redonda?

Cálculo:

P_c = (4 − 1)! = 3! = 3×2×1 = 6

Portanto, há 6 maneiras de organizar as 4 pessoas ao redor da mesa.

4. Permutação Circular com Repetição

A permutação circular com repetição ocorre quando elementos repetidos são organizados em um círculo. Nesse caso, a fórmula ajusta o cálculo para levar em conta tanto as repetições quanto as redundâncias causadas pela rotação.

Fórmula:

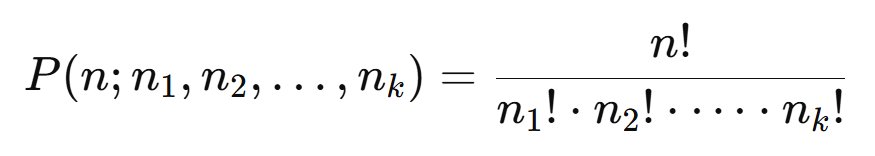
Onde:

• n: número total de elementos.
• n1, n2, …, nk: número de repetições de cada elemento.

Exemplo Prático:

Quantas formas distintas podemos organizar 5 bolas em um círculo, sendo 3 pretas (P) e 2 brancas (B)?

Solução:

1. Total de bolas (n): 5.
2. Repetições:
   • Bolas pretas (n₁ = 3).
   • Bolas brancas (n₂ = 2).
3. Substitua na fórmula:

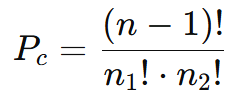
Substituindo os valores temos:

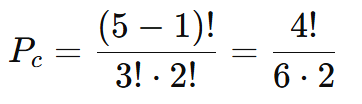
Calcule os fatoriais:

• 4! = 4×3×2×1 = 24
• 3! = 6
• 2! = 2

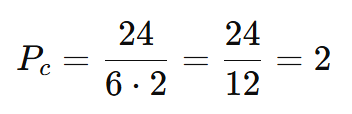
Resposta: Existem 2 arranjos únicos.

Exemplo Prático:

Quantas maneiras diferentes podemos organizar 7 flores em uma coroa circular, sendo 3 flores vermelhas e 3 flores brancas e uma rosa?

1 – Análise Combinatória – Permutação Circular com Repetição
Neste problema, estamos organizando 7 flores em uma coroa circular, sendo:

• 3 flores vermelhas,
• 3 flores brancas,
• 1 flor rosa.

Como a disposição é circular e há repetições, utilizamos a fórmula da Permutação Circular com Repetição:

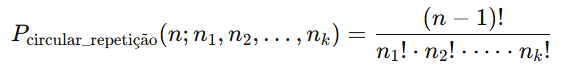
2 – Entendendo o Enunciado

1. Total de flores (n=7n = 7).
2. Repetições:
   • 3 flores vermelhas (n₁ = 3),
   • 3 flores brancas (n₂ = 3),
   • 1 flor rosa (n₃ = 1).

Aplicamos a fórmula considerando as repetições e a disposição circular.

3 – Cálculo

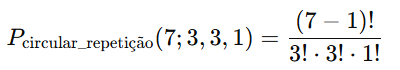
Calculamos os fatoriais:

(7−1)! = 6! = 720

3! = 6,

1! = 1.

Substituímos:

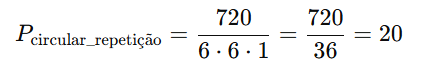
4 – Resposta
As 7 flores (3 vermelhas, 3 brancas e 1 rosa) podem ser organizadas em uma coroa circular de 20 maneiras diferentes.

👉Entre no nosso canal do WhatsApp

📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito

Comparação Entre os Tipos de Permutação

Tipo	Descrição	Fórmula
Permutação Simples	Organização linear de elementos distintos.	P(n) = n!
Permutação com Repetição	Organização linear com elementos repetidos.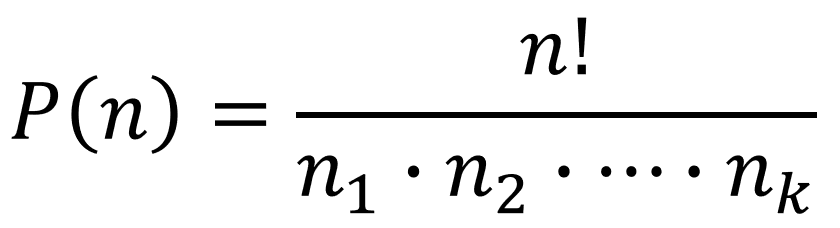
Permutação Circular	Organização em círculo com elementos distintos.	Pc = (n – 1)!
Permutação Circular com Repetição	Organização em círculo com elementos repetidos.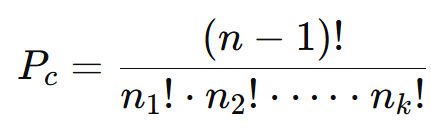

Aplicações Práticas das Permutações

1. Planejamento e Organização:
   Quantas formas diferentes você pode organizar os convidados em uma mesa de jantar? Use permutação simples para descobrir!
2. Segurança Digital:
   Ao criar senhas com caracteres únicos, as permutações ajudam a calcular o número total de combinações possíveis.
3. Jogos e Competição:
   Determinar a ordem de participantes em uma competição ou a sequência de rodadas em jogos.

Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!

Conclusão

As permutações são um dos conceitos mais intuitivos e úteis da análise combinatória assim como a combinação e o arranjo. Elas aparecem em diversas situações práticas, desde tarefas simples como organizar objetos, até cenários mais complexos, como a criação de sistemas de segurança.

Entender a diferença entre permutação simples e com elementos repetidos é essencial dentro da matemática para aplicar o conceito de forma eficaz. Com a prática, calcular permutações se torna uma ferramenta poderosa para resolver problemas do dia a dia.