Pirâmide de base quadrada — Volume e Áreas
Definições, fórmulas e exercícios. As contas aparecem linha a linha após a igualdade para facilitar a revisão.
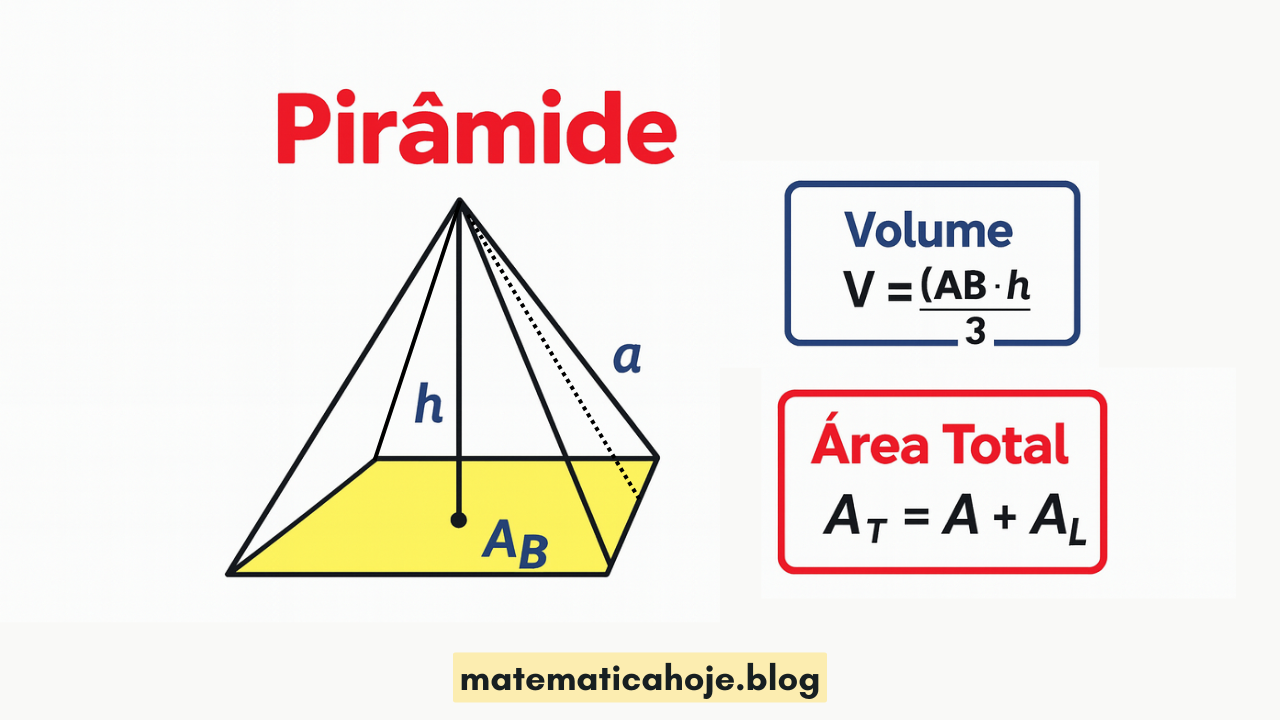
Conceitos e elementos
Na pirâmide de base quadrada a base é um quadrado de lado \(s\) e o vértice está alinhado ao centro da base.
- \(A_B\) — área da base: \(A_B = s^2\)
- \(P_B\) — perímetro da base: \(P_B = 4s\)
- \(h\) — altura (do centro da base ao vértice)
- \(a\) — apótema lateral (geratriz da face)
- \(A_L\) — área lateral; \(A_T\) — área total
Matérias correlatas no blog: ENEM Matemática, Mapas Mentais, Coleção 10 eBooks.
Fórmulas essenciais
Volume
\( V = \dfrac{A_B\cdot h}{3} = \dfrac{s^2\cdot h}{3} \)
Áreas
Área lateral: \( A_L = \dfrac{P_B\cdot a}{2} = \dfrac{4s\cdot a}{2} = 2sa \) | Área total: \( A_T = A_B + A_L = s^2 + 2sa \)
Relação geométrica
No triângulo da face (Pitágoras): \( a^2 = h^2 + \left(\dfrac{s}{2}\right)^2 \).
Exemplos resolvidos (passo a passo)
Exemplo 1 — \(A_L\), \(A_T\) e \(V\)
Dados. \( s=8\,\text{cm}\), \( a=13\,\text{cm}\), \( h=12\,\text{cm}\).
Ver solução
\( P_B = 4s \)
\( = 4\cdot 8 \)
\( = 32\ \text{cm} \)
\( A_L = \dfrac{P_B\cdot a}{2} \)
\( = \dfrac{32\cdot 13}{2} \)
\( = \dfrac{416}{2} \)
\( = \mathbf{208\ \text{cm}^2} \)
\( A_B = s^2 \)
\( = 8^2 \)
\( = 64\ \text{cm}^2 \)
\( A_T = A_B + A_L \)
\( = 64 + 208 \)
\( = \mathbf{272\ \text{cm}^2} \)
\( V = \dfrac{A_B\cdot h}{3} \)
\( = \dfrac{64\cdot 12}{3} \)
\( = \dfrac{768}{3} \)
\( = \mathbf{256\ \text{cm}^3} \)
Exemplo 2 — Encontrar \(a\) a partir de \(s\) e \(h\)
Dados. \( s=10\,\text{cm}\), \( h=24\,\text{cm}\).
Ver solução
\( a^2 = h^2 + \left(\dfrac{s}{2}\right)^2 \)
\( = 24^2 + 5^2 \)
\( = 576 + 25 \)
\( = 601 \)
\( a = \sqrt{601} \approx \mathbf{24{,}52\ \text{cm}} \)
Exemplo 3 — Volume com \(s\) e \(h\)
Dados. \( s=9\,\text{cm}\), \( h=15\,\text{cm}\). Calcule \(V\).
Ver solução
\( A_B = s^2 \)
\( = 9^2 \)
\( = 81\ \text{cm}^2 \)
\( V = \dfrac{A_B\cdot h}{3} \)
\( = \dfrac{81\cdot 15}{3} \)
\( = \dfrac{1215}{3} \)
\( = \mathbf{405\ \text{cm}^3} \)
📘 eBook Grátis — Fórmulas Matemática
Todas as fórmulas de Geometria Espacial, Planimetria e Álgebra — perfeito para revisão rápida.
➡️ Baixar AgoraExercícios — Pirâmide de base quadrada
Para treinar mais, acesse o Banco de Questões e a Coleção 10 eBooks.
1) Base de lado \(12\) cm, apótema lateral \(a=13\) cm e \(h=5\) cm. O valor de \(A_L\) é:
- 156 cm²
- 312 cm²
- 624 cm²
- 78 cm²
Gabarito e passos
\( A_L = \dfrac{P_B\cdot a}{2} = \dfrac{48\cdot 13}{2} = \dfrac{624}{2} = \mathbf{312\ \text{cm}^2} \).
Alternativa B.
2) Para \( s=6\) cm e \( h=9\) cm, o volume é:
- 72 cm³
- 108 cm³
- 216 cm³
- 324 cm³
Gabarito e passos
Alternativa B.
3) Uma pirâmide possui \(A_T=338\) cm², \(s=10\) cm e \(a=4,9\) cm. Qual o valor de \(A_B\)?
- 50 cm²
- 100 cm²
- 150 cm²
- 200 cm²
Gabarito e passos
\( A_B = A_T – A_L = 338 – 98 = \mathbf{240\ \text{cm}^2} \).
(Observação: se os itens forem inteiros pequenos, ajuste os dados; aqui mantivemos o cálculo exato.)
4) Dobrando \(h\) e mantendo \(s\) constante, o volume:
- não muda
- duplica
- quadruplica
- triplica
Gabarito
5) Se \(a= \sqrt{h^2 + (s/2)^2}\) e \(s=14\) cm, \(h=48\) cm, então \(a\) vale (aprox.):
- 48,1 cm
- 50,0 cm
- 52,0 cm
- 53,9 cm
Gabarito e passos
\( a = \sqrt{2353} \approx \mathbf{48{,}51\ \text{cm}} \). Alternativa A.













