Pirâmide de base regular — Volume e Áreas
Definições, fórmulas e exercícios. As contas aparecem linha a linha após a igualdade para facilitar a revisão.
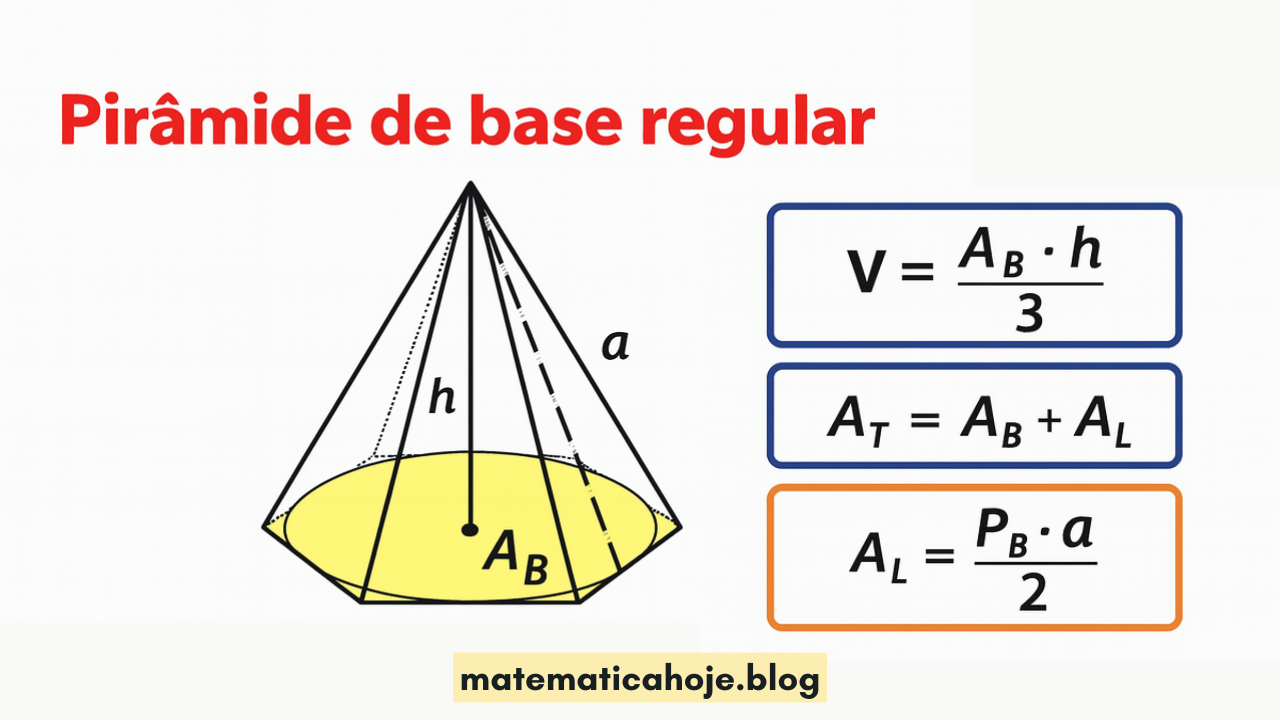
Conceitos e elementos
Chamamos de pirâmide de base regular aquela cuja base é um polígono regular (todos os lados e ângulos iguais) e cujo vértice está alinhado ao centro da base.
- \(A_B\) — área da base.
- \(P_B\) — perímetro da base.
- \(h\) — altura (do centro da base ao vértice).
- \(a\) — apótema lateral (geratriz da face; distância do vértice ao meio de um lado da base).
- \(A_L\) — área lateral; \(A_T\) — área total.
Conteúdo recorrente no ENEM Matemática. Para revisar de forma visual, use os Mapas Mentais.
Fórmulas essenciais
Volume
\( V = \dfrac{A_B\cdot h}{3} \)
Áreas
Área lateral: \( A_L = \dfrac{P_B\cdot a}{2} \) | Área total: \( A_T = A_B + A_L \)
Para base regular de lado \(s\) e número de lados \(n\): \(P_B = n\,s\). Fórmulas úteis de área de base: triângulo equilátero \( \left(\dfrac{\sqrt{3}}{4}s^2\right)\), quadrado \((s^2)\), hexágono regular \(\left(\dfrac{3\sqrt{3}}{2}s^2\right)\).
Relação entre \(a\), \(h\) e a base
Na face, vale Pitágoras:
\( a^2 = h^2 + r^2 \), onde \(r\) é a distância do centro ao meio do lado da base.
Para base quadrada \(s\): \( r = \dfrac{s}{2} \).
Exemplos resolvidos (passo a passo)
Exemplo 1 — Base quadrada (com \(a\))
Enunciado. Pirâmide de base quadrada com lado \( s=8\,\text{cm}\), apótema lateral \( a=13\,\text{cm}\) e altura \( h=12\,\text{cm}\). Calcule \(A_L\), \(A_T\) e \(V\).
Ver solução
\( P_B = 4s \)
\( = 4\cdot 8 \)
\( = 32\ \text{cm} \)
\( A_L = \dfrac{P_B\cdot a}{2} \)
\( = \dfrac{32\cdot 13}{2} \)
\( = \dfrac{416}{2} \)
\( = \mathbf{208\ \text{cm}^2} \)
\( A_B = s^2 \)
\( = 8^2 \)
\( = 64\ \text{cm}^2 \)
\( A_T = A_B + A_L \)
\( = 64 + 208 \)
\( = \mathbf{272\ \text{cm}^2} \)
\( V = \dfrac{A_B\cdot h}{3} \)
\( = \dfrac{64\cdot 12}{3} \)
\( = \dfrac{768}{3} \)
\( = \mathbf{256\ \text{cm}^3} \)
Exemplo 2 — Encontrando \(a\) (base quadrada)
Enunciado. Pirâmide de base quadrada de lado \( s=10\,\text{cm}\) e altura \( h=24\,\text{cm}\). Calcule o apótema lateral \( a \).
Ver solução
\( r = \dfrac{s}{2} \)
\( = \dfrac{10}{2} \)
\( = 5\ \text{cm} \)
\( a^2 = h^2 + r^2 \)
\( = 24^2 + 5^2 \)
\( = 576 + 25 \)
\( = 601 \)
\( a = \sqrt{601} \approx \mathbf{24{,}52\ \text{cm}} \)
Exemplo 3 — Base hexagonal (volume)
Enunciado. Base: hexágono regular de lado \( s=6\,\text{cm}\). Altura \( h=10\,\text{cm}\). Calcule \( V \).
Ver solução
\( A_B = \dfrac{3\sqrt{3}}{2}\,s^2 \)
\( = \dfrac{3\sqrt{3}}{2}\cdot 6^2 \)
\( = \dfrac{3\sqrt{3}}{2}\cdot 36 \)
\( = 54\sqrt{3}\ \text{cm}^2 \)
\( V = \dfrac{A_B\cdot h}{3} \)
\( = \dfrac{54\sqrt{3}\cdot 10}{3} \)
\( = 180\sqrt{3} \)
\( \approx \mathbf{311{,}77\ \text{cm}^3} \)
📘 eBook Grátis — Fórmulas Matemática
Todas as fórmulas de Geometria Espacial, Planimetria e Álgebra — perfeito para revisão rápida.
➡️ Baixar AgoraExercícios — Pirâmide de base regular
Para treinar mais, acesse o Banco de Questões e a Coleção 10 eBooks.
1) Pirâmide de base quadrada com lado \(12\) cm, apótema lateral \(a=13\) cm e altura \(h=5\) cm. O valor de \(A_L\) é:
- 156 cm²
- 312 cm²
- 624 cm²
- 78 cm²
Gabarito e passos
\( A_L = \dfrac{P_B\cdot a}{2} = \dfrac{48\cdot 13}{2} = \dfrac{624}{2} = \mathbf{312\ \text{cm}^2} \).
Alternativa B.
2) Uma pirâmide regular tem base hexagonal de lado \(6\) cm e \(h=9\) cm. O volume é:
- 81√3 cm³
- 108√3 cm³
- 162√3 cm³
- 243√3 cm³
Gabarito e passos
\( V = \dfrac{A_B\cdot h}{3} = \dfrac{54\sqrt{3}\cdot 9}{3} = 162\sqrt{3} \).
Alternativa C.
3) Numa pirâmide de base quadrada \(s=10\) cm, se \(h=24\) cm então o apótema lateral é (aprox.):
- 20,0 cm
- 22,4 cm
- 24,5 cm
- 26,0 cm
Gabarito e passos
\( a = \sqrt{h^2 + r^2} = \sqrt{24^2 + 5^2} = \sqrt{576+25} = \sqrt{601}\approx \mathbf{24{,}52\ \text{cm}} \).
Alternativa C.
4) Para uma pirâmide regular, dobrar \(h\) e manter \(A_B\) constante faz o volume:
- dobrar
- triplicar
- quadruplicar
- não mudar
Gabarito
5) Se \(A_L = 180\) cm² e \(a=9\) cm, então o perímetro da base é:
- 10 cm
- 15 cm
- 20 cm
- 40 cm
Gabarito e passos
\( = \dfrac{2\cdot 180}{9} \)
\( = \dfrac{360}{9} \)
\( = \mathbf{40\ \text{cm}} \). Alternativa D.













